题目内容
求y=
+sinx-sin2x，x∈R的最大最小值．
| 7 |
| 4 |
考点：三角函数的最值
专题：三角函数的求值
分析：先利用配方法整理函数解析式，进而个sinx的范围确定函数的最值．
解答：
解：y=
+sinx-sin2x=-（sinx-
）2+2，
∵-1≤sinx≤1，
∴当sinx=-1时，函数取得最小值：-
，
当sinx=
时，函数取得最大值：2
| 7 |
| 4 |
| 1 |
| 2 |
∵-1≤sinx≤1，
∴当sinx=-1时，函数取得最小值：-
| 1 |
| 4 |
当sinx=
| 1 |
| 2 |
点评：本题主要考查了三角函数的最值以及二次函数的性质．解题的关键时利用函数的思想来解决问题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
等比数列{an}的首项为1，公比为q，前n项和为S，则数列{
}的前n项之和为（ ）
| 1 |
| an |
A、
| ||
| B、S | ||
| C、S•q1-n | ||
| D、S-1•q1-n |
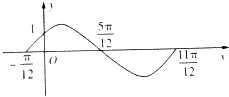函数f1（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
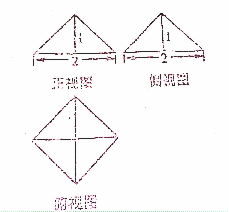某几何体的三视图如图所示，其中正视图、侧视图均为斜边等于2的等腰直角三角形，俯视图是对角线为2的正方形，则该几何体的内切球的半径等于