Question

定义在R上的奇函数f（x），当x≥0时，f（x）=

-x2，x∈[0，1) 1-|x-3|，x∈[1，+∞)

，则方程f（x）=

1

4

的所有解之和为

 

．

Answer 1

考点：根的存在性及根的个数判断,函数奇偶性的性质

专题：函数的性质及应用

分析：根据奇函数f（x）在x≥0时的解析式，结合图象及其对称性得，左边两根之和为-6，最右边两根之和为6，中间的一个根为-

1

2

，从而得到答案．

解答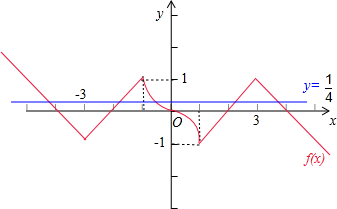： 解：先作出当x≥0时，f（x）=

-x2，x∈[0，1) 1-|x-3|，x∈[1，+∞)

的图象，再根据f（x）为奇函数，它的图象关于原点对称，
可得它在R上的图象，如图所示：设函数f（x）与直线y=

1

4

的5个交点的横坐标从左向右分别为x₁、x₂、x₃、x₄、x₅，
则由图象的对称性可得 x₁+x₂=-6，x₄+x₅=6，再由

y=x2(-1≤x＜0) y= 1 4

，求得x=-

1

2

，故x₃=-

1

2

，
∴方程f（x）=

1

4

的所有解之和为 为x₁+x₂+x₃+x₄+x₅=-

1

2

，
故答案为：-

1

2

．

点评：本题考查分段函数的意义，求函数解析式，利用函数图象的性质，体现数形结合、转化的数学思想，属于基础题．