题目内容
已知函数f(x)=2x2+3(a2+a)lnx-8ax
(Ⅰ)若x=3是f(x)的一个极值点求a的值;
(Ⅱ)若函数f(x)在其导函数f(x)′的单调区间上也是单调的,求a的取值范围.
(Ⅰ)若x=3是f(x)的一个极值点求a的值;
(Ⅱ)若函数f(x)在其导函数f(x)′的单调区间上也是单调的,求a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(I)f′(x)=4x+
-8a=
,则f′(3)=4(3-a)2-a2+3a=0,验证求a;
(II)f′(x)=4x+
-8a=
,讨论f′(x)的单调性,从而求解.
| 3(a2+a) |
| x |
| 4(x-a)2-a2+3a |
| x |
(II)f′(x)=4x+
| 3(a2+a) |
| x |
| 4x2-8ax+3(a2+a) |
| x |
解答:
解:(Ⅰ)f′(x)=4x+
-8a=
=
,
∵x=3是f(x)的一个极值,
∴f′(3)=4(3-a)2-a2+3a=0,
解得,a=4或a=3;
而当a=3时,f′(x)≥0,故不成立,
当a=4时,满足条件,
故a=4.
(II)f′(x)=4x+
-8a=
设g(x)=4x2-8ax+3(a2+a),△=16(a2-3a),
设g(x)=0的两根为x1,x2,(x1<x2),
(1)当△≤0,即0≤a≤3时,
∴f(x)单调递增,满足题意;
(2)当△>0,即a<0或a>3时,
①若x1<0<x2,则
(a2+a)<0,即-1<a<0,
此时,f(x)在(0,x2)上单调递减,
在(x2,+∞)上单调递增,
而f′(x)在(0,+∞)上单调递增,
故不满足题意,
②若x1<x2≤0,则
,
解得a≤-1,
此时,f(x)在(0,+∞)上单调递增,满足题意;
③若0<x1<x2,则
,
则a>0,
此时,f(x)在(0,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增,不满足题意;
综上所述,a的取值范围为(-∞,-1]∪[0,3].
| 3(a2+a) |
| x |
| 4x2-8ax+3(a2+a) |
| x |
=
| 4(x-a)2-a2+3a |
| x |
∵x=3是f(x)的一个极值,
∴f′(3)=4(3-a)2-a2+3a=0,
解得,a=4或a=3;
而当a=3时,f′(x)≥0,故不成立,
当a=4时,满足条件,
故a=4.
(II)f′(x)=4x+
| 3(a2+a) |
| x |
| 4x2-8ax+3(a2+a) |
| x |
设g(x)=4x2-8ax+3(a2+a),△=16(a2-3a),
设g(x)=0的两根为x1,x2,(x1<x2),
(1)当△≤0,即0≤a≤3时,
∴f(x)单调递增,满足题意;
(2)当△>0,即a<0或a>3时,
①若x1<0<x2,则
| 3 |
| 4 |
此时,f(x)在(0,x2)上单调递减,
在(x2,+∞)上单调递增,
而f′(x)在(0,+∞)上单调递增,
故不满足题意,
②若x1<x2≤0,则
|
解得a≤-1,
此时,f(x)在(0,+∞)上单调递增,满足题意;
③若0<x1<x2,则
|
则a>0,
此时,f(x)在(0,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增,不满足题意;
综上所述,a的取值范围为(-∞,-1]∪[0,3].
点评:本题考查了导数的综合应用及分类讨论的数学思想,属于难题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
将球的表面积扩大到原来的4倍,则其体积扩大到原来的( )
| A、2倍 | B、4倍 | C、8倍 | D、16倍 |
设F是双曲线
-
=1(a>0,b>0)的左焦点,A(a,b),P是双曲线右支上的动点.若|PF|+|PA|的最小值为3a,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、1+
| ||||
C、
| ||||
D、
|
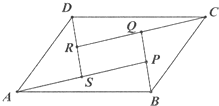 如图,在平行四边形ABCD中,设
如图,在平行四边形ABCD中,设