题目内容
16．已知集合A={x|y=$\sqrt{（1-x）（x+3）}$}，B={x|log2x≤1}，则A∩B=（ ）| A． | {x|-3≤x≤1} | B． | {x|0＜x≤1} | C． | {x|-3≤x≤2} | D． | {x|x≤2} |
分析 求出A中x的范围确定出A，求出B中不等式的解集确定出B，找出两集合的交集即可．
解答 解：由A中y=$\sqrt{（1-x）（x+3）}$，得到（1-x）（x+3）≥0，即（x-1）（x+3）≤0，
解得：-3≤x≤1，即A={x|-3≤x≤1}，
由B中不等式变形得：log2x≤1=log22，
解得：0＜x≤2，即B={x|0＜x≤2}，
则A∩B={x|0＜x≤1}，
故选：B．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
17．已知a＞b＞c，且a+b+c=0，则下列不等式中正确的是（ ）
| A． | a2＞b2＞c2 | B． | ac＞bc | C． | ab＞ac | D． | a|b|＞c|b| |
4．
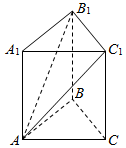如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，$A{A_1}=\sqrt{6}$，则AA1与平面AB1C1所成的角为（ ）
如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2，$A{A_1}=\sqrt{6}$，则AA1与平面AB1C1所成的角为（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
11．下列函数中满足$f（\frac{{{x_1}+{x_2}}}{2}）＜\frac{{f（{x_1}）+f（{x_2}）}}{2}（{x_1}≠{x_2}）$的是（ ）
| A． | f（x）=ax+b | B． | f（x）=xα | C． | f（x）=logax（a＞0，a≠1） | D． | f（x）=x2+ax+b |
1．如果复数$\frac{3-bi}{2+i}$（b∈R，i为虚数单位）的实部与虚部相等，则b的值为（ ）
| A． | 1 | B． | -6 | C． | 3 | D． | -9 |
如图所示，BC是半圆O的直径，AD⊥BC，垂足为D，$\widehat{AB}=\widehat{AF}$，BF与AD、AO分别交于点E、G．
6．已知$\overrightarrow a=（λ+1，0，2λ）$，$\overrightarrow b=（6，2μ-1，2）$，若$\overrightarrow a⊥\overrightarrow b$，则λ的值为（ ）
| A． | $\frac{3}{5}$ | B． | $-\frac{3}{5}$ | ||
| C． | $-\frac{1}{10}$ | D． | 不确定，与μ值相关 |