Question

已知A、B、C三点共线，O为直线外任意一点，且

OA

=m

OB

+n

OC

（m，n＞0），则

1

m

+

9

n

的最小值为

 

．

Answer 1

考点：基本不等式,平面向量的基本定理及其意义

专题：不等式的解法及应用,平面向量及应用

分析：利用向量共线定理可得m+n=1，再利用“乘1法”和基本不等式即可得出．

解答： 解：如图所示，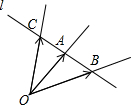
∵A、B、C三点共线，
∴存在实数λ使得

BA

=λ

AC

，（λ＞0）．
∴

OA

=

OB

+λ(

OC

-

OA

)，
化为

OA

=

1

1+λ

OB

+

λ

1+λ

OC

，
与

OA

=m

OB

+n

OC

（m，n＞0）比较可得，
m=

1

1+λ

，n=

λ

1+λ

，
∴m+n=

1

1+λ

+

λ

1+λ

=1．
∴

1

m

+

9

n

=（m+n）(

1

m

+

9

n

)=10+

n

m

+

9m

n

≥10+2

n m • 9m n

=16，
当且仅当n=3m=

3

4

时取等号．
因此

1

m

+

9

n

的最小值为16．
故答案为：16．

点评：本题考查了向量共线定理、“乘1法”和基本不等式的性质，考查了推理能力和计算能力，属于难题．