题目内容
14.函数f(x)=loga$\frac{1-x}{1+x}$(0<a<1).(1)求函数f(x)的定义域D,并判断f(x)的奇偶性;
(2)如果当x∈(t,a)时,f(x)的值域为(-∞,1),求a与t的值.
分析 (1)根据真数大于0,可得函数的定义域,根据对数的运算性质,可得f(-x)=-f(x)得:f(x)为奇函数;
(2)由f(x)的值域为(-∞,1)求出相应的自变量的取值范围,可得a与t的值.
解答 解:(1)由$\frac{1-x}{1+x}$>0得:x∈(-1,1),
故函数f(x)的定义域D=(-1,1);
由函数f(x)的定义域关于原点对称,
且f(-x)=loga$\frac{1+x}{1-x}$=-loga$\frac{1-x}{1+x}$=-f(x)得:f(x)为奇函数;
(2)∵0<a<1,
故f(x)的值域为(-∞,1)时,$\frac{1-x}{1+x}$>a,
即$\frac{(a+1)x+(a-1)}{x+1}<0$,
解得:x∈(-1,$\frac{1-a}{a+1}$),
∴t=-1,a=$\frac{1-a}{a+1}$,
解得:a=$\frac{-1+\sqrt{2}}{2}$,或a=$\frac{-1-\sqrt{2}}{2}$(舍去),
综上:a=$\frac{-1+\sqrt{2}}{2}$,t=-1
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
相关题目
4.设l,m,n为三条不同的直线,α为一个平面,下列命题中正确的是( )
①若l⊥α,则l与α相交
②若m?α,n?α,l⊥m,l⊥n,则l⊥α
③若l∥m,m∥n,l⊥α,则n⊥α
④若l∥m,m⊥α,n⊥α,则l∥n.
①若l⊥α,则l与α相交
②若m?α,n?α,l⊥m,l⊥n,则l⊥α
③若l∥m,m∥n,l⊥α,则n⊥α
④若l∥m,m⊥α,n⊥α,则l∥n.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
2.曲线$f(x)=\frac{1}{2}{x^2}$的斜率为1的切线方程为( )
| A. | 2x+2y+1=0 | B. | 2x+2y-1=0 | C. | 2x-2y-1=0 | D. | 2x-2y-3=0 |
19.某制药公司研制出一种新流感疫苗,为测试该疫苗的有效性,公司选定3000个流感样本分成三组,测试结果如下表:
已知在全体样本中随机抽取1个,抽取B组的概率是$\frac{1}{3}$
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取600个测试结果,问应在C组抽取多少个?
(3)若疫苗有效的概率不小于99%,则认为测试通过,已知y≥885,求不能通过测试的概率.
| A组 | B组 | C组 | |
| 疫苗有效 | 903 | x | y |
| 疫苗无效 | 197 | 90 | z |
(1)求x的值;
(2)现用分层抽样的方法在全体样本中抽取600个测试结果,问应在C组抽取多少个?
(3)若疫苗有效的概率不小于99%,则认为测试通过,已知y≥885,求不能通过测试的概率.
6.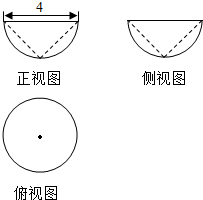 如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )
如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )
 如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )
如图为一个半球挖去一个圆锥后的几何体的三视图,则剩余部分与挖去部分的体积之比为( )| A. | 3:1 | B. | 2:1 | C. | 1:1 | D. | 1:2 |
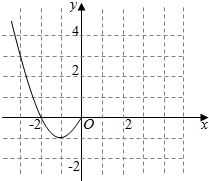 已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象:
已知函数f(x)是定义在R上的偶函数,现已画出函数f(x)在y轴左侧的图象,如图所示,请根据图象: