题目内容
3．函数y=$\left\{\begin{array}{l}{kx+1（-2≤x≤0）}\\{2sin（ωx+φ）（ω＞0，0＜x≤\frac{8π}{3}）}\end{array}\right.$的图象如图，则k=$\frac{1}{2}$，ω=$\frac{1}{2}$，φ=$\frac{π}{6}$．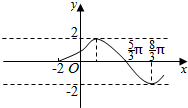
分析 由直线y=kx+1过点（-2，0）得k=$\frac{1}{2}$；可确定$\frac{T}{4}$=$\frac{8π}{3}$-$\frac{5π}{3}$=π，从而确定ω=$\frac{1}{2}$，再代入点求φ即可．
解答 解：∵直线y=kx+1过点（-2，0），
∴k=$\frac{1}{2}$；
∵$\frac{T}{4}$=$\frac{8π}{3}$-$\frac{5π}{3}$=π，
∴T=4π，
∴ω=$\frac{2π}{4π}$=$\frac{1}{2}$，
（$\frac{8π}{3}$，-2）代入y=2sin（$\frac{1}{2}$x+φ）得，
sin（$\frac{4π}{3}$+φ）=-1，
解得，φ=$\frac{π}{6}$；
故答案为：$\frac{1}{2}$，$\frac{1}{2}$，$\frac{π}{6}$．
点评 本题考查了分段函数及数形结合的思想应用．
练习册系列答案
相关题目
13．已知$sinα=-\frac{1}{4}，a∈（π，\frac{3π}{2}），cosβ=\frac{4}{5}，β∈（\frac{3π}{2}，2π）$，则α+β是（ ）
| A． | 第一象限角 | B． | 第二象限角 | C． | 第三象限角 | D． | 第四象限角 |
11．下列函数中，既是奇函数又是增函数的是（ ）
| A． | y=x|x| | B． | y=x2，x∈[-1，1] | ||
| C． | $y=-\frac{1}{x}，x∈[{-1，0}）∪（{0，1}）$ | D． | y=x+1 |
如图，已知M、N、P分别是△ABC三边BC、CA、AB上的点，且$\overrightarrow{BM}$=$\frac{1}{4}$$\overrightarrow{BC}$，$\overrightarrow{CN}$=$\frac{1}{4}$$\overrightarrow{CA}$，$\overrightarrow{AP}$=$\frac{1}{4}$$\overrightarrow{AB}$，如果$\overrightarrow{AB}$=a，$\overrightarrow{AC}$=b，选择基底{a，b}