题目内容
7.母线长为1的圆锥的侧面展开图的圆心角为$\frac{4}{3}$π,则该圆锥的体积是( )| A. | $\frac{2\sqrt{5}}{81}$π | B. | $\frac{4\sqrt{5}}{27}$π | C. | $\frac{4\sqrt{5}}{81}$π | D. | $\frac{\sqrt{10}}{81}$π |
分析 求出圆锥的侧面展开图扇形的弧长,再求底面半径,求出圆锥的高,即可求它的体积.
解答 解:圆锥的侧面展开图扇形的弧长,即底面圆的周长为$\frac{4}{3}$π•1=$\frac{4}{3}$π,于是设底面圆的半径为r,
则有2πr=$\frac{4}{3}$π,所以r=$\frac{2}{3}$,
于是圆锥的高为h=$\sqrt{1-{r}^{2}}$=$\sqrt{1-(\frac{2}{3})^{2}}$=$\frac{\sqrt{5}}{3}$,
该圆锥的体积为:$\frac{1}{3}$×($\frac{2}{3}$)2π×$\frac{\sqrt{5}}{3}$=$\frac{4\sqrt{5}}{81}$π.
故选:C.
点评 本题考查圆锥的体积,考查计算能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知函数f(x)=sinx-cosx,把f(x)的图象左移$\frac{π}{4}$个单位,得到g(x)的图象,则g(x)的解析式为( )
| A. | g(x)=$\sqrt{2}$sinx | B. | g(x)=-$\sqrt{2}$sinx | C. | g(x)=$\sqrt{2}$cosx | D. | g(x)=-$\sqrt{2}$cosx |
15.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}(x+1),x>0}\\{2f(x+4),x≤0}\end{array}\right.$,则f(-2)=2.
12.某校开展研究性学习活动需组成指导教师团队,决定用分层抽样的方法从高一、高二、高三三个年级相关教师中抽取,有关数据如下表:(单位:人)
(Ⅰ)求x、y;
(Ⅱ)现要从高二、高三抽取的教师中选取2人作讲座,求这2位教师都来自高三的概率.
| 年级 | 相关教师数 | 抽取教师数 |
| 高一 | x | 4 |
| 高二 | 12 | 2 |
| 高三 | 18 | y |
(Ⅱ)现要从高二、高三抽取的教师中选取2人作讲座,求这2位教师都来自高三的概率.

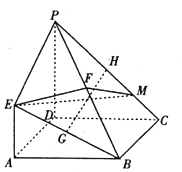 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,G、H分别为BP、BE、PC的中点.