题目内容
若正项等比数列{an}的公比为q,且q≠1,a3,
a5,a4成等差数列,则
= .
| 1 |
| 2 |
| a3+a5 |
| a4+a6 |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:由题意和等差中项的性质列出方程,求出公比q的值,再由等比数列的通项公式化简
,最后代入求值.
| a3+a5 |
| a4+a6 |
解答:
解:因为a3,
a5,a4成等差数列,
所以a5=a3+a4,则a3q2=a3+a3q,
即q2-q-1=0,解得q=
,
又等比数列{an}的各项为正项,所以q=
,
则
=
=
=
=
,
故答案为:
.
| 1 |
| 2 |
所以a5=a3+a4,则a3q2=a3+a3q,
即q2-q-1=0,解得q=
1±
| ||
| 2 |
又等比数列{an}的各项为正项,所以q=
1+
| ||
| 2 |
则
| a3+a5 |
| a4+a6 |
| a3+a3q2 |
| a3q+a3q3 |
| 1 |
| q |
| 2 | ||
1+
|
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查等比数列的通项公式,等差中项的性质,考查化简计算能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,在圆O中,已知弦AB=4,弦AC=6,那么
如图,在圆O中,已知弦AB=4,弦AC=6,那么| AO |
| BC |
| A、10 | ||
B、2
| ||
C、
| ||
| D、-10 |
已知a,b为异面直线,则下列命题中正确的是( )
| A、过a,b外一点P一定可以引一条与a,b都平行的直线 |
| B、过a,b外一点P一定可以作一个与a,b都平行的平面 |
| C、过a一定可以作一个与b平行的平面 |
| D、过a一定可以作一个与b垂直的平面 |
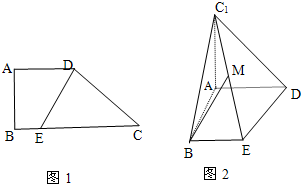 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=