题目内容
将一个边长为3,4,5的直角三角形绕斜边旋转一周得到一个旋转体,问该旋转体的表面积为 .
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:由题意,所求旋转体由两个同底的圆锥拼接而成.利用解三角形知识,算出圆锥的底面半径,结合锥体的侧面公式得到旋转体的表面积S=
,.
| 84π |
| 5 |
解答:
解: 根据题意,所求旋转体由两个同底的圆锥拼接而成
根据题意,所求旋转体由两个同底的圆锥拼接而成
它的底面半径等于直角三角形斜边上的高,高分别等于两条直角边在斜边的射影长
∵两直角边边长分别为3和4,
∴斜边长为
=5,
由面积公式可得斜边上的高为h=
=
可得所求旋转体的底面半径r=
因此,两个圆锥的侧面积分别为
S上侧面=π×
×4=
;S下侧面=π×
×3=
∴旋转体的表面积S=
+
=
故答案为:
.
 根据题意,所求旋转体由两个同底的圆锥拼接而成
根据题意,所求旋转体由两个同底的圆锥拼接而成它的底面半径等于直角三角形斜边上的高,高分别等于两条直角边在斜边的射影长
∵两直角边边长分别为3和4,
∴斜边长为
| 32+42 |
由面积公式可得斜边上的高为h=
| 3×4 |
| 5 |
| 12 |
| 5 |
可得所求旋转体的底面半径r=
| 12 |
| 5 |
因此,两个圆锥的侧面积分别为
S上侧面=π×
| 12 |
| 5 |
| 48π |
| 5 |
| 12 |
| 5 |
| 36π |
| 5 |
∴旋转体的表面积S=
| 48π |
| 5 |
| 36π |
| 5 |
| 84π |
| 5 |
故答案为:
| 84π |
| 5 |
点评:本题考查的是圆锥的计算,以直角三角形斜边所在的直线为轴转动一周,得到的几何体是两个圆锥,用圆锥的表面积公式求出这个几何体表面积.

练习册系列答案
相关题目
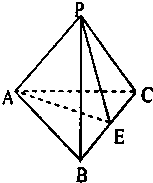 如图所示,点P是平面ABC外一点,且满足PA、PB、PC两两垂直,PE⊥BC,则该图中两两垂直的平面共有( )
如图所示,点P是平面ABC外一点,且满足PA、PB、PC两两垂直,PE⊥BC,则该图中两两垂直的平面共有( )| A、3对 | B、4对 | C、5对 | D、6对 |
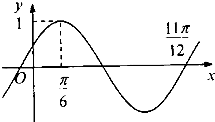 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|