题目内容
下列命题中正确的是（ ）
| A、空间中的任意三点确定一个平面 |
| B、空间中两两相交的三条直线确定一个平面 |
| C、有且只有一组对边平行的四边形是平面图形 |
| D、两组对边分别相等的四边形一定是平面图形 |
考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：利用平面的基本性质及其推论求解．
解答：
解：A中，共线的三点确定无数个平面，故A错误；
B中，空间中两两相交的三条直线确定一个平面或三个平面，故B错误；
C中，因为两条平行线确定一个平面，
所以有且只有一组对边平行的四边形是平面图形，故C正确；
D中，两组对边分别相等的四边形有可能是空间四边形，故D不正确．
故选：C．
B中，空间中两两相交的三条直线确定一个平面或三个平面，故B错误；
C中，因为两条平行线确定一个平面，
所以有且只有一组对边平行的四边形是平面图形，故C正确；
D中，两组对边分别相等的四边形有可能是空间四边形，故D不正确．
故选：C．
点评：本题考查命题真假的判断，是基础题，解题时要认真审题，注意平面的基本性质的灵活运用．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
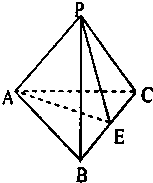如图所示，点P是平面ABC外一点，且满足PA、PB、PC两两垂直，PE⊥BC，则该图中两两垂直的平面共有（ ）| A、3对 | B、4对 | C、5对 | D、6对 |
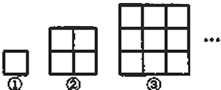如图图形都是由同样大小的正方形按一定规律组成，第①个图形中有1个正方形，第②个图形中有5个正方形，…，则第⑥个图形中正方形的个数是（ ）| A、36 | B、55 | C、70 | D、91 |
数列
，
，
，
，…的一个通项公式为（ ）
| 1 |
| 3 |
| 1 |
| 8 |
| 1 |
| 15 |
| 1 |
| 24 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|
有一个几何体的三视图如图所示，这个几何体是一个（ ）
| A、棱台 | B、棱锥 | C、棱柱 | D、圆台 |
极坐标平面内，集合P={（ρ，θ）|sinθ=-
，ρ∈R}与集合S={（ρ，θ）|cosθ=
，ρ∈R}之间的关系是（ ）
| 1 |
| 2 |
| ||
| 2 |
| A、P?S |
| B、P?S |
| C、P=S |
| D、P∩S={（0，0）} |
| ∫ | 1 0 |
| 1-(x-1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|