题目内容

2．已知向量$\overrightarrow{a}$=（2，m）与向量$\overrightarrow{b}$=（-1，-2）共线，则实数的值是4．

分析 利用向量共线定理即可得出．

解答 解：∵向量$\overrightarrow{a}$=（2，m）与向量$\overrightarrow{b}$=（-1，-2）共线，
∴-m-2×（-2）=0，
解得m=4．
故答案为：4．

点评 本题考查了向量共线定理，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
12．已知方程x2-2ax+a2-4=0的一个实根在区间（-1，0）内，另一个实根大于2，则实数a的取值范围是（　　）
A．0＜a＜4B．1＜a＜2C．-2＜a＜2D．a＜-3或a＞1
13．若一个扇形的圆心角为$\frac{π}{3}$，所在圆的半径为2，则这个扇形的面积为$\frac{2π}{3}$．
10．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+ax-2，}&{x≤1}\\{lo{g}_{a}x，}&{x＞1}\end{array}\right.$在R上单调递增，则实数a的取值范围是（　　）
A．0＜a≤3B．a≥2C．2≤a≤3D．0＜a≤2或a≥3
17．命题“?x0∈R，x${\;}_{0}^{2}$+2x0≥2”的否定为（　　）
A．?x0∈R，${x}_{0}^{2}$+2x0≤2B．?x∈R，x2+2x≥2
C．?x0∈R，${x}_{0}^{2}$+2x0＜2D．?x∈R，x2+2x＜2
7．在抛物线y2=2px（p＞0）中有如下结论：过焦点F的动直线l交抛物线y2=2px（p＞0）于A、B两点，则$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=f（x）为定值，请把此结论类比到椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$中有：过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的焦点F的直线交椭圆于A，B则$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=$\frac{2a}{b^2}$为定值；当椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1时，$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=$\frac{4}{3}$．
14．在△ABC中，a，b，c分别是角A，B，C的对边，$cosB=\frac{3}{5}$且$\overrightarrow{BA}•\overrightarrow{BC}=21$
（1）求△ABC的面积；
（2）若a=7，求角C．
11．函数f（x）=log2（x+1）与g（x）=2-x+1在同一直角坐标系下的图象大致是（　　）
A．B．C．D．
12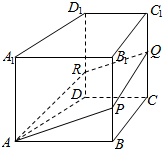．如图，在四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD，AB∥CD，∠DCB=90°，AB=AD=AA1=2DC，Q为棱CC1上一动点，过直线AQ的平面分别与棱BB1，DD1交于点P，R，则下列结论错误的是（　　）
A．对于任意的点Q，都有AP∥QR
B．对于任意的点Q，四边形APQR不可能为平行四边形
C．存在点Q，使得△ARP为等腰直角三角形
D．存在点Q，使得直线BC∥平面APQR

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网