题目内容
12.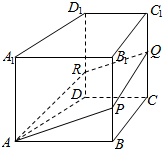 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,∠DCB=90°,AB=AD=AA1=2DC,Q为棱CC1上一动点,过直线AQ的平面分别与棱BB1,DD1交于点P,R,则下列结论错误的是( )
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,AB∥CD,∠DCB=90°,AB=AD=AA1=2DC,Q为棱CC1上一动点,过直线AQ的平面分别与棱BB1,DD1交于点P,R,则下列结论错误的是( )| A. | 对于任意的点Q,都有AP∥QR | |
| B. | 对于任意的点Q,四边形APQR不可能为平行四边形 | |
| C. | 存在点Q,使得△ARP为等腰直角三角形 | |
| D. | 存在点Q,使得直线BC∥平面APQR |
分析 根据面面平行的性质判断A,B,使用假设法判断C,D.
解答 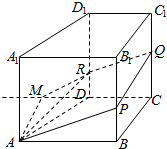 解:(1)∵AB∥CD,AA1∥DD1,
解:(1)∵AB∥CD,AA1∥DD1,
∴平面ABB1A1∥平面CDD1C1,∵平面APQR∩平面ABB1A1=AP,平面APQR∩平面CDD1C1=RQ,
∴AP∥QR,故A正确.
(2)∵四边形ABCD是直角梯形,AB∥CD,∴平面BCC1B1与平面ADD1A1不平行,
∵平面APQR∩平面BCC1B1=PQ,平面APQR∩平面ADD1A1=AR,
∴PQ与AR不平行,故四边形APQR不可能为平行四边形,故B正确.
(3)延长CD至M,使得DM=CM,则四边形ABCM是矩形,∴BC∥AM.
当R,Q,M三点共线时,AM?平面APQR,∴BC∥平面APQR,故D正确.
故选C.
点评 本题考查了直棱柱的结构特征,面面平行的性质,线面平行的判定,属于中档题.

练习册系列答案
相关题目
3.已知F是抛物线y2=4x的焦点,P1,P2,P3是该抛物线上的点,它们的横坐标依次为x1,x2,x3,若x1,x2,x3成等比数列且log2x1+log2x2+log2x3=3,则|P2F|=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
17.下列命题中正确的个数为( )
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②残差平方和越小的模型,模型拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好.
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②残差平方和越小的模型,模型拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
4.已知m,n为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是( )
| A. | m∥n,m⊥α⇒n⊥α | B. | α∥β,m?α,n?β⇒m∥n | ||
| C. | m?α,n?β,m∥n⇒α∥β | D. | m?α,n?α,m∥β,n∥β⇒α∥β |
1.在平面直角坐标系中,已知A(1,0),B(3,2),则直线AB的倾斜角大小( )
| A. | 30° | B. | 45° | C. | 135° | D. | 150° |