题目内容
已知圆M：x2+（y-1）2=1，过圆心M的直线与抛物线x2=4y及圆M的交点依次为A，B，C，D，则|AC|•|BD|的取值范围为（ ）
| A、（9，+∞） |
| B、[9，+∞） |
| C、（4，+∞） |
| D、[4，+∞） |
考点：抛物线的简单性质,直线与圆的位置关系
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：设A（x1，y1），B（x2，y2），运用抛物线的定义，结合圆的定义，可得|AC|•|BD|=（y1+2）（y2+2），设直线AD：x=m（y-1），代入抛物线方程，运用韦达定理，化简整理，即可得到m的关系式，即可得到范围．
解答：
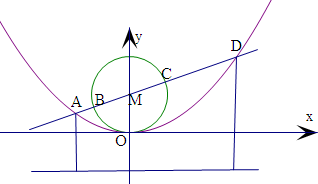解：设A（x1，y1），B（x2，y2），
抛物线x2=4y的焦点为（0，1），准线为y=-1．
|AM|=y1+1，|DM|=y2+1，
则|AB|=|AM|-1=y1，|CD|=|DM|-1=y2，
则有|AC|•|BD|=（y1+2）（y2+2）
=y1y2+2（y1+y2）+4
设直线AD：x=m（y-1），代入抛物线方程，
得，m2y2-（2m2+4）y+m2=0，
即有y1+y2=2+
，y1y2=1，
则|AC|•|BD|=1+4+
+4=9+
＞9．
故选A．
解：设A（x1，y1），B（x2，y2），抛物线x2=4y的焦点为（0，1），准线为y=-1．
|AM|=y1+1，|DM|=y2+1，
则|AB|=|AM|-1=y1，|CD|=|DM|-1=y2，
则有|AC|•|BD|=（y1+2）（y2+2）
=y1y2+2（y1+y2）+4
设直线AD：x=m（y-1），代入抛物线方程，
得，m2y2-（2m2+4）y+m2=0，
即有y1+y2=2+
| 4 |
| m2 |
则|AC|•|BD|=1+4+
| 8 |
| m2 |
| 8 |
| m2 |
故选A．
点评：本题考查抛物线的定义和方程及性质，考查直线和抛物线方程联立消去未知数，运用韦达定理解题，考查运算能力，属于中档题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
如图，正方体的底面与正四面体的底面在同一平面α上，且棱AB所在的直线与棱CD所在的直线互相平行，正方体的六个面所在的平面与直线CE、EF相交的平面个数分别记为m，n，那么m=