题目内容
计算:(lg1+lg2+lg4+lg8+…+lg1024)•log210= .
考点:对数的运算性质
专题:函数的性质及应用
分析:利用对数的运算法则、指数的运算法则、等差数列的前n项和公式即可得出.
解答:
解:(lg1+lg2+lg4+lg8+…+lg1024)•log210=lg(2×4×…×1024)•log210=lg21+2+…+10
=
=55.
故答案为:55.
| 1 |
| lg2 |
| 10(1+10) |
| 2 |
故答案为:55.
点评:本题考查了对数的运算法则、指数的运算法则、等差数列的前n项和公式,属于基础题.

练习册系列答案
相关题目
已知圆M:x2+(y-1)2=1,过圆心M的直线与抛物线x2=4y及圆M的交点依次为A,B,C,D,则|AC|•|BD|的取值范围为( )
| A、(9,+∞) |
| B、[9,+∞) |
| C、(4,+∞) |
| D、[4,+∞) |
已知点A(n,m)和点B(n+1,t)在二次函数y=x2的图象上,n为正整数,直线AB与x轴所成的锐角的大小为α,则tanα=( )
| A、n+1 | B、2n+1 |
| C、n-1 | D、2n-1 |
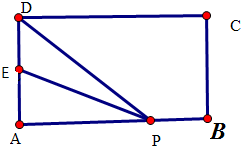 如图,在矩形ABCD中,E是AD的中点,P是AB边上的点,AB=3,AD=2
如图,在矩形ABCD中,E是AD的中点,P是AB边上的点,AB=3,AD=2