题目内容
已知椭圆C1:
+
=1,其左准线为l1,右准线为l2,抛物线C2以坐标原点O为顶点,l2为准线,C2交l1于A,B两点.
(1)求抛物线C2的标准方程;
(2)求线段AB的长度.
| x2 |
| 4 |
| y2 |
| 3 |
(1)求抛物线C2的标准方程;
(2)求线段AB的长度.
考点:椭圆的简单性质,抛物线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)设抛物线C2的标准方程为y2=-2px(P>0).由椭圆C1:
+
=1,其左准线为l1:x=-4,右准线为l2:x=4.因此
=4,解得p即可得出抛物线C2的标准方程.
(2)联立
,解出即可得出线段|AB|的长度.
| x2 |
| 4 |
| y2 |
| 3 |
| p |
| 2 |
(2)联立
|
解答:
解:(1)设抛物线C2的标准方程为y2=-2px(P>0).
由椭圆C1:
+
=1,可得:a2=4,b2=3,c=
=1,
∴其左准线为l1:x=-4,右准线为l2:x=4.
∴
=4,解得p=8.
∴抛物线C2的标准方程为y2=-16x.
(2)联立
,解得
,
.
∴线段|AB|=16.
由椭圆C1:
| x2 |
| 4 |
| y2 |
| 3 |
| a2-b2 |
∴其左准线为l1:x=-4,右准线为l2:x=4.
∴
| p |
| 2 |
∴抛物线C2的标准方程为y2=-16x.
(2)联立
|
|
|
∴线段|AB|=16.
点评:本题考查了椭圆与抛物线的标准方程及其性质,属于基础题.

练习册系列答案
相关题目
如图Rt△O′A′B′是一平面图形的直观图,直角边O′B′=2,则这个平面图形的面积是( )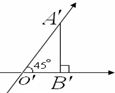

A、2
| ||
| B、1 | ||
C、4
| ||
D、
|
已知圆M:x2+(y-1)2=1,过圆心M的直线与抛物线x2=4y及圆M的交点依次为A,B,C,D,则|AC|•|BD|的取值范围为( )
| A、(9,+∞) |
| B、[9,+∞) |
| C、(4,+∞) |
| D、[4,+∞) |
已知点A(n,m)和点B(n+1,t)在二次函数y=x2的图象上,n为正整数,直线AB与x轴所成的锐角的大小为α,则tanα=( )
| A、n+1 | B、2n+1 |
| C、n-1 | D、2n-1 |
下列说法不正确的是( )
A、“cosα=
| ||||
| B、命题P:?x∈R,使得x2+x-1<0,则p:?x∈R,使得x2+x-1≥0 | ||||
| C、命题“在△ABC中,若A>B,则sinA>sinB”的逆否命题是真命题 | ||||
| D、若p∧q为假命题,则p∨q为假命题 |