题目内容
过点P(6,-1),在x轴、y轴上的截距分别为a、b,且满足a=3b的直线方程为 .
考点:直线的截距式方程
专题:计算题
分析:设出直线方程,求出a,b,利用a=3b,求出直线的斜率,然后求出直线方程.
解答:
解:设直线的斜率为k,所以直线方程为:y=k(x-6)-1.
由题意可知a=
+6,b=-6k-1,因为a=3b,所以
+6=3(-6k-1),
解得k=-
或k=-
,
故所求的直线方程为:y=-
x+1或y=-
x.
故答案为:y=-
x+1或y=-
x.
由题意可知a=
| 1 |
| k |
| 1 |
| k |
解得k=-
| 1 |
| 3 |
| 1 |
| 6 |
故所求的直线方程为:y=-
| 1 |
| 3 |
| 1 |
| 6 |
故答案为:y=-
| 1 |
| 3 |
| 1 |
| 6 |
点评:本题考查直线方程的求法,直线的截距式方程的应用,考查计算能力.

练习册系列答案
相关题目
函数y=x4-4x+3在区间[-1,2]上的最大值为( )
| A、11 | B、8 | C、12 | D、0 |
已知幂函数y=f(x)图象经过点(4,
),则f(3)=( )
| 1 |
| 2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
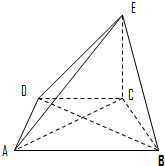 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.