题目内容
15.设i是虚数单位,则$\frac{{{{({1+i})}^3}}}{{{{({1-i})}^2}}}$=-1-i.分析 直接利用复数代数形式的乘除运算化简得答案.
解答 解:$\frac{{{{({1+i})}^3}}}{{{{({1-i})}^2}}}$=$\frac{(1+i)^{2}(1+i)}{(1-i)^{2}}=\frac{2i(1+i)}{-2i}=-1-i$.
故答案为:-1-i.
点评 本题考查复数代数形式的乘除运算,是基础题.

练习册系列答案
相关题目
6.已知命题p:?x∈R,x2+2ax+a≤0.若命题p是假命题,则实数a的取值范围是( )
| A. | a<0或a>1 | B. | a≤0或a≥1 | C. | 0≤a≤1 | D. | 0<a<1 |
3.用秦九韶算法求多项式f(x)=x6+6x4+9x2+208在x=-4时,v2的值为( )
| A. | -4 | B. | 1 | C. | 17 | D. | 22 |
7.经过点A(1,1),并且在两坐标轴上的截距的绝对值相等的直线有( )
| A. | 0条 | B. | 1条 | C. | 2条 | D. | 3条 |
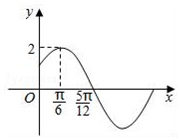 已知函数f(x)=Asin(ωx+φ)
已知函数f(x)=Asin(ωx+φ)