题目内容
11.已知tanx=-4,求sin2x及sinx cosx的值.分析 由题意利用同角三角函数的基本关系,求得要求式子的值.
解答 解:∵tanx=-4,∴sin2x=$\frac{{sin}^{2}x}{{sin}^{2}x{+cos}^{2}x}$=$\frac{{tan}^{2}x}{{tan}^{2}x+1}$=$\frac{16}{17}$,
sinx cosx=$\frac{sinxcosx}{{sin}^{2}x{+cos}^{2}x}$=$\frac{tanx}{{tan}^{2}x+1}$=-$\frac{4}{17}$.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
16.已知随机变量ξ~B(10,0.6),则E(ξ),D(ξ)分别是( )
| A. | 6和2.4 | B. | 4和2.4 | C. | 4和3.6 | D. | 6和1.6 |
20.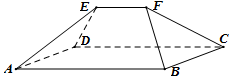 《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )| A. | $8\sqrt{3}$ | B. | $8+8\sqrt{3}$ | C. | $6\sqrt{2}+2\sqrt{3}$ | D. | $8+6\sqrt{2}+2\sqrt{3}$ |
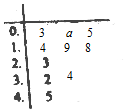 已知函数f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,现有一组数据(该组数据数量庞大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.
已知函数f(x)=x2+$\sqrt{2}$(m-1)x+$\frac{m}{4}$,现有一组数据(该组数据数量庞大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.