题目内容
已知函数f(x)=xex-x-2在区间[k,k+1]上有解,则实数k的取值集合是 .
考点:根的存在性及根的个数判断,利用导数研究函数的单调性
专题:函数的性质及应用
分析:由f(x)=0得ex=
=1+
,然后分别作出函数y=ex,与y=1+
的图象,利用数形结合即可得到结论.
| x+2 |
| x |
| 2 |
| x |
| 2 |
| x |
解答:
解:当x=0时,f(0)=-2<0,∴0不是函数的零点,
当x≠0,由f(x)=xex-x-2=0得xex=x+2,
即ex=
=1+
,
设函数y=ex,与y=1+
,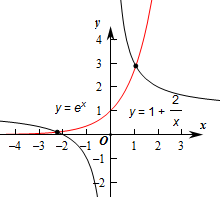 分别作出函数y=ex,与y=1+
分别作出函数y=ex,与y=1+
的图象如图:
由图象可知两个函数的交点个数为2个,
由图象可知函数零点所在的区间分别为[-3,-2]和[1,2]上,
故k=-3或k=1,
即实数k的取值集合是{-3,1},
故答案为:{-3,1}
当x≠0,由f(x)=xex-x-2=0得xex=x+2,
即ex=
| x+2 |
| x |
| 2 |
| x |
设函数y=ex,与y=1+
| 2 |
| x |
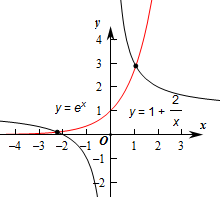 分别作出函数y=ex,与y=1+
分别作出函数y=ex,与y=1+| 2 |
| x |
由图象可知两个函数的交点个数为2个,
由图象可知函数零点所在的区间分别为[-3,-2]和[1,2]上,
故k=-3或k=1,
即实数k的取值集合是{-3,1},
故答案为:{-3,1}
点评:本题主要考查函数零点个数的判断,根据函数和方程之间的关系,转化为两个函数图象的交点个数问题,利用数形结合是解决本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
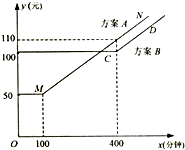 移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).
移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等). 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.