题目内容
若三棱锥P-ABC,AP,BP,CP两两垂直,AP=CP=2,BP=
,则P到面ABC的距离是 .
| 5 |
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:取AC中点D,连结BD,PD,作PO⊥平面ABC,交BD于点O,由已知条件推导出在△PBD中,PD2+PB2=BD2,由
BD•PO=
PD•PB,能求出P到面ABC的距离PO.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:如图,三棱锥P-ABC,AP,BP,CP两两垂直,
AP=CP=2,BP=
,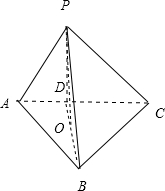
取AC中点D,连结BD,PD,作PO⊥平面ABC,交BD于点O,
AB=BC=
=3,AC=
=2
,
PD=
=
,BD=
=
,
在△PBD中,PD2+PB2=BD2,
∴
BD•PO=
PD•PB,
∴P到面ABC的距离PO=
=
=
.
故答案为:
.
AP=CP=2,BP=
| 5 |

取AC中点D,连结BD,PD,作PO⊥平面ABC,交BD于点O,
AB=BC=
| 5+4 |
| 4+4 |
| 2 |
PD=
| 4-2 |
| 2 |
| 9-2 |
| 7 |
在△PBD中,PD2+PB2=BD2,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴P到面ABC的距离PO=
| PD•PB |
| BD |
| ||||
|
| ||
| 7 |
故答案为:
| ||
| 7 |
点评:本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
