题目内容
在平面直角坐标系xOy中,已知点A(-6,0),B(4,0),C(9,m),△ABC的外接圆为⊙M.
(1)若∠CAB=30°,求m值;
(2)若⊙M与直线l:ax+2y+6=0相切于点A,求⊙M的方程;
(3)若⊙M与y轴交于P、Q两点,求PQ长的最小值.
(1)若∠CAB=30°,求m值;
(2)若⊙M与直线l:ax+2y+6=0相切于点A,求⊙M的方程;
(3)若⊙M与y轴交于P、Q两点,求PQ长的最小值.
考点:直线与圆的位置关系,圆的标准方程
专题:直线与圆
分析:(1)首先,根据∠CAB=30°,结合直角三角形中边角关系,求解m的值;
(2)先将A(-6,0)代入所给直线方程,求解得到a的值,然后,求解过圆心且和已知直线垂直的直线方程,最后,联立方程组,求解圆的圆心,从而得到其方程;
(3)首先设圆心坐标,然后,根据圆的弦长公式求解弦长的表达式,最后确定其最值.
(2)先将A(-6,0)代入所给直线方程,求解得到a的值,然后,求解过圆心且和已知直线垂直的直线方程,最后,联立方程组,求解圆的圆心,从而得到其方程;
(3)首先设圆心坐标,然后,根据圆的弦长公式求解弦长的表达式,最后确定其最值.
解答:
解:(1)∵∠CAB=30°,
∴
=tan30°=
,
∴|m|=5
,
∴m=±5
,
∴m值为±5
;
(2)∵A(-6,0),
将该点坐标代人直线方程,得
a(-6)+2×0+6=0,
解得a=1,
∴直线方程为:x+2y+6=0,
与上述直线垂直且切点为(-6,0)的直线方程为:
2x-y-12=0,
联立方程组
,
解得
,
∴圆心坐标为(-1,10),
半径为r=
=5
,
∴⊙M的方程(x+1)2+(y-10)2=125.
(3)设圆心为(-1,b),
则当圆M与直线x=9相切时,r最小,
此时PQ长取得最小值,
此时r=10,圆心到PQ的距离为1,
PQ=2
=6
,
∴PQ长的最小值6
.
∴
| |m| |
| 15 |
| ||
| 3 |
∴|m|=5
| 3 |
∴m=±5
| 3 |
∴m值为±5
| 3 |
(2)∵A(-6,0),
将该点坐标代人直线方程,得
a(-6)+2×0+6=0,
解得a=1,
∴直线方程为:x+2y+6=0,
与上述直线垂直且切点为(-6,0)的直线方程为:
2x-y-12=0,
联立方程组
|
解得
|
∴圆心坐标为(-1,10),
半径为r=
| (-1+6)2+(10-0)2 |
| 5 |
∴⊙M的方程(x+1)2+(y-10)2=125.
(3)设圆心为(-1,b),
则当圆M与直线x=9相切时,r最小,
此时PQ长取得最小值,
此时r=10,圆心到PQ的距离为1,
PQ=2
| 102-12 |
| 11 |
∴PQ长的最小值6
| 11 |
点评:本题重点考查了圆的性质、直线与圆的位置关系等知识,属于中档题,解题关键是准确掌握圆的性质和直线方程.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
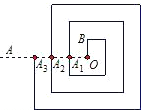 如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、
如图是一回形图,其回形通道的宽和OB的长均为1,回形线与射线OA交于A1、A2、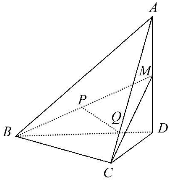 如图,四面体A-BCD中,AD⊥面BCD,BC⊥CD,AD=2,BD=2
如图,四面体A-BCD中,AD⊥面BCD,BC⊥CD,AD=2,BD=2