题目内容
13.已知平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都等于2,且两两夹角为60°,则对角线BD1的长度为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | $\frac{{\sqrt{3}}}{2}+2$ |
分析 根据平行六面体法则可得:$\overrightarrow{{BD}_{1}}$=$\overrightarrow{BA}$+$\overrightarrow{{BB}_{1}}$+$\overrightarrow{BC}$,先求出两两向量的夹角,再利用模的计算公式即可得出
解答 解:∵共顶点A的三条棱两两所成的角为60°,
∴∠ABC=120°=∠ABB1,∠CBB1=60°,
又各条棱长均为2,
∴$\overrightarrow{BA}$•$\overrightarrow{BC}$=$\overrightarrow{BA}$•$\overrightarrow{{BB}_{1}}$=2×2×cos120°=-2,$\overrightarrow{BC}$•$\overrightarrow{{BB}_{1}}$=2×2×cos60°=2.
∵$\overrightarrow{{BD}_{1}}$=$\overrightarrow{BA}$+$\overrightarrow{{BB}_{1}}$+$\overrightarrow{BC}$,
∴$\overrightarrow{{BD}_{1}}$2=($\overrightarrow{BA}$+$\overrightarrow{{BB}_{1}}$+$\overrightarrow{BC}$)2=$\overrightarrow{BA}$2+$\overrightarrow{{BB}_{1}}$2+$\overrightarrow{BC}$2+2$\overrightarrow{BA}$•$\overrightarrow{{BB}_{1}}$+2 $\overrightarrow{BA}$•$\overrightarrow{BC}$+2 $\overrightarrow{BC}$•$\overrightarrow{{BB}_{1}}$=4+4+4+2×(-2)×2+2×2=8,
∴|$\overrightarrow{{BD}_{1}}$|=2$\sqrt{2}$.
故选:A.
点评 本题考查的知识点是向量在几何中的应用,熟练掌握平行六面体法则及模的计算公式是解题的关键

| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 4 |
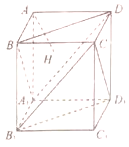 如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )
如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )