题目内容
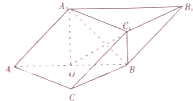 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.(Ⅰ)在线段CC1上是否存在点D,使得OD∥平面A1C1B,若存在,证明你的结论;若不存在,说明理由;
(Ⅱ)若AA1=A1B=AC=BC,AA1与平面ABC所成的角为
| π |
| 4 |
考点:与二面角有关的立体几何综合题,棱锥的结构特征,直线与平面平行的性质
专题:空间位置关系与距离
分析:(Ⅰ)线段CC1上存在点D,当D为线段CC1中点时,OD∥平面A1C1B.取BC中点E,连结OD、DE、OE,由三角形中位线定理能证明平面ODE∥平面A1C1B,从而得到OD∥平面A1C1B.
(Ⅱ)取AC中点F,连结OF,FA1,AA1与平面ABC所成的角为∠A1AB=45°,由已知条件推导出∠OA1F是二面角O-A1C1-A的平面角,由此能求出二面角O-A1C1-A的正切值.
(Ⅱ)取AC中点F,连结OF,FA1,AA1与平面ABC所成的角为∠A1AB=45°,由已知条件推导出∠OA1F是二面角O-A1C1-A的平面角,由此能求出二面角O-A1C1-A的正切值.
解答:
解:(Ⅰ)线段CC1上存在点D,当D为线段CC1中点时,OD∥平面A1C1B.
证明如下:
取BC中点E,连结OD、DE、OE,
∵DE是△BCC1的中位线,∴DE∥BC1,
∵OE是△ABC的中位线,
∴OE∥AC,又AC∥A1C1,∴OE∥A1C1,
∴平面ODE∥平面A1C1B,
∵OD?平面ODE,∴OD∥平面A1C1B.
(Ⅱ)取AC中点F,连结OF,FA1,
∵AA1=A1B,O是AB的中点,∴A1O⊥AB,
又平面A1ABB1⊥平面ABC,∴A1O⊥平面ABC,
则AA1与平面ABC所成的角为∠A1AB=45°,
且A1O⊥AC,
∵AA1=A1B=AC=BC,
∴△A1AB ,△ABC均为等腰直角三角形,
∵OF是△ABC的中位线,∴OF⊥AC.
∴AC⊥平面A1OF,
∵AC∥A1C1,∴A1C1⊥平面A1OF,
∴A1C1⊥OG,∴A1C1⊥AO,
∴∠OA1F是二面角O-A1C1-A的平面角,
在Rt△A1OF中,OF=
BC,A1O=
BC,
∴tan∠OA1F=
.
证明如下:
取BC中点E,连结OD、DE、OE,

∵DE是△BCC1的中位线,∴DE∥BC1,
∵OE是△ABC的中位线,
∴OE∥AC,又AC∥A1C1,∴OE∥A1C1,
∴平面ODE∥平面A1C1B,
∵OD?平面ODE,∴OD∥平面A1C1B.
(Ⅱ)取AC中点F,连结OF,FA1,
∵AA1=A1B,O是AB的中点,∴A1O⊥AB,
又平面A1ABB1⊥平面ABC,∴A1O⊥平面ABC,
则AA1与平面ABC所成的角为∠A1AB=45°,
且A1O⊥AC,
∵AA1=A1B=AC=BC,
∴△A1AB ,△ABC均为等腰直角三角形,
∵OF是△ABC的中位线,∴OF⊥AC.
∴AC⊥平面A1OF,
∵AC∥A1C1,∴A1C1⊥平面A1OF,
∴A1C1⊥OG,∴A1C1⊥AO,
∴∠OA1F是二面角O-A1C1-A的平面角,
在Rt△A1OF中,OF=
| 1 |
| 2 |
| ||
| 2 |
∴tan∠OA1F=
| ||
| 2 |
点评:本题考查满足直线与平面平行的点是否存在的判断,考查二面角的正切值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
执行图示的程序框图,如果输入的x∈[-2,2],则输出的y属于( )

A、[
| ||
B、(
| ||
C、[
| ||
D、(
|
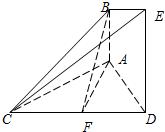 如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点. 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.