题目内容
已知某物体的运动曲线方程为：S=2t2-3t-1，则该物体在t=3时的速度为（ ）
| A、8 | B、9 | C、10 | D、11 |
考点：变化的快慢与变化率
专题：
分析：此类运动问题中瞬时速度问题的研究一般借助函数的导数求其某一时刻的瞬时速度，解答本题可以先求质点的运动方程为s（t）=2t2-3t-1的导数，再求得t=3秒时的导数，即可得到所求的瞬时速度
解答：
解∵质点的运动方程为s（t）=2t2-3t-1
∴s′（t）=4t-3
∴该质点在t=3秒的瞬时速度为4×3-3=9米/秒．
故选B．
∴s′（t）=4t-3
∴该质点在t=3秒的瞬时速度为4×3-3=9米/秒．
故选B．
点评：本题考查变化的快慢与变化率，正确解答本题关键是理解导数的物理意义，即了解函数的导数与瞬时速度的关系，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目
△ABC中A，B，C的对边分别是a，b，c，若
=
，（b+c+a）（b+c-a）=3bc，则△ABC的形状为（ ）
| sinA |
| sinB |
| a |
| c |
| A、等边三角形 |
| B、等腰非等边三角形 |
| C、直角三角形 |
| D、钝角三角形 |
已知圆C1：(x+1)2+(y-1)2=1，圆C2与圆C1关于直线x-y=0对称，则圆C2的方程为（ ）
| A、（x-1）2+（y+1）2=1 |
| B、（x-1）2+（y-1）2=1 |
| C、（x+1）2+（y+1）2=1 |
| D、（x+1）2+（y-1）2=1 |
已知△ABC中，AB=
，BC=1，sinC=
cosC，则△ABC的面积为（ ）
| 3 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设z=1-i（i是虚数单位），则复数
+i2的实部是（ ）
| 3 |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
若P是抛物线x2=4y上的一个动点，则点P到直线l1：y=-1，l2：3x+4y+12=0的距离之和的最小值为（ ）
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
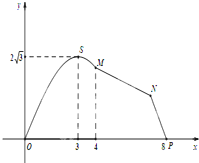如图，某市拟在长为8km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y=Asin（ωx）（A＞0，ω＞0），x∈[0，4]的图象，且图象的最高点为S（3，2
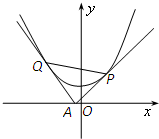过x轴上动点A（a，0），引抛物线y=x2+1的两条切线AP、AQ．切线斜率分别为k1和k2，切点分别为P、Q．