题目内容
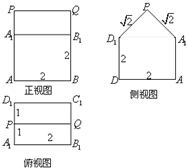 某一几何体的三视图如图所示.按照给出的尺寸(单位:cm):
某一几何体的三视图如图所示.按照给出的尺寸(单位:cm):(1)请写出该几何体是由哪些简单几何体组合而成的;
(2)求出这个几何体的体积.
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:(1)根据三视图,得该几何体是在棱长为2的正方体上面放置一个直三棱柱,
(2)该三棱柱的底面是直角边为
的等腰直角三角形,高等于2,且它的一个边长为2的正方形侧面与下部正方体吻合.由此不难得到该几何体积的体积.
(2)该三棱柱的底面是直角边为
| 2 |
解答:
解:(1)根据三视图,得该几何体的形状是由两部分组成:
上部分是底面是两条直角边都等于
的等腰直角三角形、高等于2的直三棱柱,
下部分是棱长为2的正方体,
(2)由(1)可得:该组合体的体积:
V=(
×
×
×2)+2×2×2=10(cm3).
上部分是底面是两条直角边都等于
| 2 |
下部分是棱长为2的正方体,
(2)由(1)可得:该组合体的体积:
V=(
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题考查的知识点是由三视图求体积,其中根据已知的三视图分析出几何体的形状是解答的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一位母亲纪录了儿子3到9岁的身高数据(略),她根据这些数据建立的身高y(cm)与年龄x的回归模型为
=7.19x+73.93,用此模型预测孩子10岁时的身高,则有( )
 |
| y |
| A、身高一定是145.83cm |
| B、身高在145.83cm左右 |
| C、身高在145.83cm以上 |
| D、身高在145.83cm以下 |
平面向量
,
中,若
=(4,-3),|
|=1,且
•
=5,则向量
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
A、(
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|