题目内容
函数y=k（1-x）和y=
（k≠0）在同一平面直角坐标系中的图象可能是（ ）
| k |
| x |
A、 |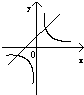
B、 |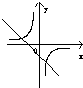
C、 |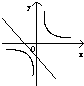
D、 |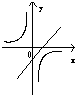
考点：函数的图象
专题：函数的性质及应用
分析：根据一次函数和分式函数的图象和性质即可得到结论．
解答：
解：函数y=k（1-x）过定点（1，0），故排除A，B，C，
在D中，k＜0，满足条件，
故选：D
在D中，k＜0，满足条件，
故选：D
点评：本题主要考查函数图象的识别和判断，根据一次函数和分式函数的图象和性质是解决本题的关键，比较基础．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
若函数f（x）满足f（x）f（x+2）=2且f（2）=2，则f（2014）=（ ）
| A、-2 | B、-1 | C、2 | D、2014 |
已知sinα+cosα=
，则sin2α=（ ）
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
下列说法错误的是（ ）
| A、若变量y和x之间的相关系数为r=-0.9362，则变量y和x之间具有线性相关关系 | ||||
B、线性回归方程对应的直线y=
| ||||
| C、在独立性检验时，两个变量的2×2列表中对角线上的乘积相差越大，说明这两个变量没有关系的可能性越大 | ||||
| D、在回归分析中，R2为0.98的模型比R2为0.80的模型拟合的效果好 |
两个平行于底面的截面将棱锥的侧面积分成三个相等的部分，则该两个截面将棱锥的高分成三段（自上而下）之比是（ ）
A、1：
| ||||||
B、1：（
| ||||||
C、1：（
| ||||||
D、1：（
|
设△ABC的内角A，B，C所对的边分别为a，b，c，若三边的长为连续的三个正整数，且A＞B＞C，A=2C，且3b=20acosA，则sinA：sinB：sinC为（ ）
| A、4：3：2 |
| B、5：4：3 |
| C、6：5：4 |
| D、7：6：5 |
在△ABC中，若2a=b+c，sin2A=sinBsinC，则△ABC一定是（ ）
| A、锐角三角形 |
| B、正三角形 |
| C、等腰直角三角形 |
| D、非等腰三角形 |