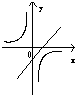题目内容
已知定义在R上的函数f（x）满足f（x+4）=f（x），且f（x）=
，则当t∈[
，3]，方程f（x）=log2|x|最多有几个实根（ ）
|
| 5 |
| 2 |
| A、7个 | B、9个 |
| C、11个 | D、13个 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：由函数f（x）满足f（x+4）=f（x），可得函数的周期为4，作出函数f（x）和y=log2|x|的图象，利用数形结合即可得到结论．
解答：
解：∵f（x+4）=f（x），
∴函数的周期为4，
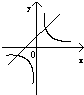
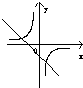
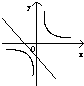
分别作出函数f（x）和y=log2|x|的图象如图：
则由图象可知，两个函数的图象交点个数为11个，
故选：C．
解：∵f（x+4）=f（x），∴函数的周期为4，
分别作出函数f（x）和y=log2|x|的图象如图：
则由图象可知，两个函数的图象交点个数为11个，
故选：C．
点评：本题主要考查方程根的个数的判断，利用函数的周期性，结合方程和函数之间的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
计算：
+（3-π）0=（ ）
| (3-π)2 |
| A、4-π | B、π-4 |
| C、2-π | D、π-2 |
已知|
|=3
，|
|=6，且
+
与
垂直，则
与
的夹角是（ ）
| a |
| 2 |
| b |
| a |
| b |
| a |
| a |
| b |
| A、30° | B、90° |
| C、45° | D、135° |
设x，y∈（0，2]，且xy=2，若6-2x-y≥a（2-x）（4-y）恒成立，则实数a的取值范围是（ ）
A、（
| ||
| B、（-∞，1] | ||
| C、[0，2） | ||
| D、（-∞，-1] |