题目内容
已知y=
cos2x+
sinxcosx+1,x∈R
(1)当y取最大值时,求x的集合
(2)若x∈[0,
],求函数的值域
(3)该函数的图象可由y=sinx经过怎样的平移变化和伸缩变化得到?
| 1 |
| 2 |
| ||
| 2 |
(1)当y取最大值时,求x的集合
(2)若x∈[0,
| π |
| 2 |
(3)该函数的图象可由y=sinx经过怎样的平移变化和伸缩变化得到?
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)根据题意利用三角函数的恒等变换化简函数的解析式为y=
sin(2x+
)+
,由此利用正弦函数的值域求得函数的最大值.
(2)由x∈[0,
],利用正弦函数的定义域和值域求得f(x)的值域.
(3)根据y=Asin(ωx+φ)的图象变换规律,得出结论.
| 1 |
| 2 |
| π |
| 6 |
| 5 |
| 4 |
(2)由x∈[0,
| π |
| 2 |
(3)根据y=Asin(ωx+φ)的图象变换规律,得出结论.
解答:
解:(1)y=
cos2x+
sinxcosx+1=
cos2x+
sin2x+
=
sin(2x+
)+
,
故函数y的最大值为
+
=
,此时x的集合为{x|x=kπ+
,k∈Z}.
(2)若x∈[0,
],则 2x+
∈[
,
],sin(2x+
)∈[-
,1],
∴f(x)∈[1,
].
(3)把y=sinx的图象向左平移
个单位,可得函数y=sin(x+
)的图象;
再把所得图象上点的横坐标变为原来的
倍,纵坐标不变,可得函数y=sin(2x+
)的图象;
再把所得图象上点的纵坐标变为原来的
倍,横坐标不变,可得函数y=
sin(2x+
)的图象,
再把所得图象向上平移
个单位,可得函数y=sin(2x+
)的图象.
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| ||
| 4 |
| 5 |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
| 5 |
| 4 |
故函数y的最大值为
| 1 |
| 2 |
| 5 |
| 4 |
| 7 |
| 4 |
| π |
| 6 |
(2)若x∈[0,
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
∴f(x)∈[1,
| 7 |
| 4 |
(3)把y=sinx的图象向左平移
| π |
| 6 |
| π |
| 6 |
再把所得图象上点的横坐标变为原来的
| 1 |
| 2 |
| π |
| 6 |
再把所得图象上点的纵坐标变为原来的
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
再把所得图象向上平移
| 5 |
| 4 |
| π |
| 6 |
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域和值域,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第100次操作后得到的数是( )
| A、25 | B、250 |
| C、55 | D、133 |
已知f(x+1)为偶函数,且f(x)在(-∞,1)单调递增,a=f(sin
),b=f(log53),c=f(tan
)则有( )
| π |
| 6 |
| π |
| 3 |
| A、a<b<c |
| B、b<c<a |
| C、c<b<a |
| D、c<a<b |
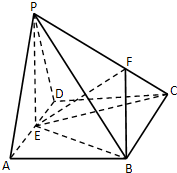 如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=
如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE= 已知函数f(x)=2cosxsin(x+
已知函数f(x)=2cosxsin(x+