题目内容
已知cos
=
,cos
cos
=
,cos
cos
cos
=
,…,根据这些结果,猜想cos
cos
cos
cos
= .
| π |
| 3 |
| 1 |
| 2 |
| π |
| 5 |
| 2π |
| 5 |
| 1 |
| 4 |
| π |
| 7 |
| 2π |
| 7 |
| 3π |
| 7 |
| 1 |
| 8 |
| π |
| 9 |
| 2π |
| 9 |
| 3π |
| 9 |
| 4π |
| 9 |
考点:归纳推理
专题:推理和证明
分析:根据已知中cos
=
,cos
cos
=
,cos
cos
cos
=
,…,归纳推理可得:cos
•cos
•…•cos
=
,进而可得答案.
| π |
| 3 |
| 1 |
| 2 |
| π |
| 5 |
| 2π |
| 5 |
| 1 |
| 4 |
| π |
| 7 |
| 2π |
| 7 |
| 3π |
| 7 |
| 1 |
| 8 |
| π |
| 2n+1 |
| 2π |
| 2n+1 |
| nπ |
| 2n+1 |
| 1 |
| 2n |
解答:
解:由已知中:
cos
=
,
cos
cos
=
,
cos
cos
cos
=
,
…,
归纳推理可得:
cos
•cos
•…•cos
=
,
当2n+1=9时,n=4,
故cos
cos
cos
cos
=
=
,
故答案为:
cos
| π |
| 3 |
| 1 |
| 2 |
cos
| π |
| 5 |
| 2π |
| 5 |
| 1 |
| 4 |
cos
| π |
| 7 |
| 2π |
| 7 |
| 3π |
| 7 |
| 1 |
| 8 |
…,
归纳推理可得:
cos
| π |
| 2n+1 |
| 2π |
| 2n+1 |
| nπ |
| 2n+1 |
| 1 |
| 2n |
当2n+1=9时,n=4,
故cos
| π |
| 9 |
| 2π |
| 9 |
| 3π |
| 9 |
| 4π |
| 9 |
| 1 |
| 24 |
| 1 |
| 16 |
故答案为:
| 1 |
| 16 |
点评:本题解答的关键是发现规律,利用规律找出一般的解决问题的方法,进一步解决问题即可.

练习册系列答案
相关题目
给定函数y=f(x)的图象如下列图中,经过原点和(1,1),且对任意an∈(0,1),由关系式an+1=f(an)得到数列{an},满足an+1>an(n∈N*),则该函数的图象为( )
A、 |
B、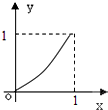 |
C、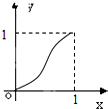 |
D、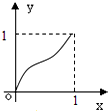 |
若有一段演绎推理:“大前提:对任意实数a,都有(
)n=a.小前提:已知a=-2为实数.结论:(
)4=-2.”这个结论显然错误,是因为( )
| n | a |
| 4 | -2 |
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、非以上错误 |
若数列{xn}满足lgxn+1=1+lgxn,且x1+x2+…+x100=100,则lg(x101+x102+…+x200)=( )
| A、102 | B、100 |
| C、1000 | D、101 |
设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.则P(ξ=0)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|