题目内容
已知函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
.
(1)求f(x)的解析式
(2)判断并用单调性的定义证明f(x)在(-1,1)上的单调性.
| kx-b |
| x2+1 |
| 1 |
| 2 |
| 4 |
| 5 |
(1)求f(x)的解析式
(2)判断并用单调性的定义证明f(x)在(-1,1)上的单调性.
考点:函数奇偶性的性质,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)由函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
.可得f(0)=0,且f(
)=
.解出即可.
(2)利用函数单调性的定义即可证明.
| kx-b |
| x2+1 |
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
(2)利用函数单调性的定义即可证明.
解答:
解:(1)∵函数f(x)=
是定义在(-1,1)上的奇函数,且f(
)=
.
∴f(0)=0,且f(
)=
.
∴
,解得b=0,k=2.
∴f(x)=
.x∈(-1,1).
(2)函数f(x)在x∈(-1,1)单调递增.
证明:?-1<x1<x2<1,则x2-x1>0,x1x2-1<0,
+1>0,
+1>0.
则f(x1)-f(x2)=
-
=
<0,
∴f(x1)<f(x2).
∴函数f(x)在x∈(-1,1)单调递增.
| kx-b |
| x2+1 |
| 1 |
| 2 |
| 4 |
| 5 |
∴f(0)=0,且f(
| 1 |
| 2 |
| 4 |
| 5 |
∴
|
∴f(x)=
| 2x |
| x2+1 |
(2)函数f(x)在x∈(-1,1)单调递增.
证明:?-1<x1<x2<1,则x2-x1>0,x1x2-1<0,
| x | 2 1 |
| x | 2 2 |
则f(x1)-f(x2)=
| 2x1 | ||
|
| 2x2 | ||
|
| 2(x2-x1)(x1x2-1) | ||
(x12+1)(
|
∴f(x1)<f(x2).
∴函数f(x)在x∈(-1,1)单调递增.
点评:本题考查了函数的奇偶性与单调性,属于基础题.

练习册系列答案
相关题目
设函数y=f(x)在R上有意义,对给定正数M,定义函数fM(x)=
,则称函数fM(x)为f(x)的“孪生函数”,若给定函数f(x)=2-x2,M=1,则y=fM(x)的值域为( )
|
| A、[1,2] |
| B、[-1,2] |
| C、(-∞,2] |
| D、(-∞,1] |
已知a,b是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A、若a∥b,b?α,则a∥α |
| B、若a∥α,b?α,则a∥b |
| C、若a⊥α,b⊥α,则a∥b |
| D、若a⊥b,b⊥α,则a∥α |
下列各组中的两个函数是同一函数的为( )
(1)y=
,y=x-5;
(2)y=
,y=
;
(3)y=|x|,y=
;
(4)y=x,y=
;
(5)y=(2x-5)2,y=|2x-5|.
(1)y=
| (x+3)(x-5) |
| x+3 |
(2)y=
| x+1 |
| x-1 |
| (x+1)(x-1) |
(3)y=|x|,y=
| x2 |
(4)y=x,y=
| 3 | x3 |
(5)y=(2x-5)2,y=|2x-5|.
| A、(1),(2) |
| B、(2),(3) |
| C、(3),(5) |
| D、(3),(4) |
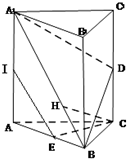 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E,I分别是CC1,AB,AA1的中点.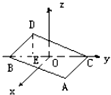 如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(
如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(