题目内容

3．在-360°～360°范围内与120°角终边相同的角为-240°．

分析 利用与α终边相同的角度为k•360°+α（k∈Z）即可得到答案．

解答 解：∵与120°角终边相同的角为：α=k•360°+120°，（k∈Z），
∵-360°～360°，
∴k=-1时，α=-240°．
故答案为：-240°

点评 本题考查与α终边相同的角的公式，考查理解与应用的能力，属于基础题．

练习册系列答案
相关题目
13．已知函数f（x）为定义在[0，3]上的减函数，则满足f（2x-1）＜f（1）的实数x的取值范围是（　　）
A．[0，1]B．（1，2]C．[$\frac{1}{2}$，2]D．（1，3]
14．已知b＞a＞0，ab=2，则$\frac{a^2+b^2}{a-b}$的取值范围是（　　）
A．（-∞，-4]B．（-∞，-4）C．（-∞，-2]D．（-∞，-2）
11．若函数f（x）=$\frac{{x}^{2}+3}{x+1}$，则函数的极值点为1，-3．
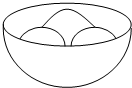18．如图，三个半径均为r的小球放在一个半球形的碗中，若三个小球的最高点恰好与碗的上沿处于同一水平面．已知这个碗的半径R=3+$\sqrt{21}$，则r=3．
8．在数列{an}中，a1=1，a2=5，an+2=an+1-an（n∈N*），则a2015=-5．
15．已知一圆的方程为f（x，y）=0，另一圆与之同心，且过点（x0，y0），求该圆方程．
12．设$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是平面的一组基底，如果$\overrightarrow{AB}$=3$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$，$\overrightarrow{BC}$=4$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$，$\overrightarrow{CD}$=8$\overrightarrow{{e}_{1}}$-9$\overrightarrow{{e}_{2}}$．求证：A，B，D三点共线．
13．“α=210°”是“sinα＜0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网