题目内容
14.已知b>a>0,ab=2,则$\frac{a^2+b^2}{a-b}$的取值范围是( )| A. | (-∞,-4] | B. | (-∞,-4) | C. | (-∞,-2] | D. | (-∞,-2) |
分析 b>a>0,ab=2,可得b>$\sqrt{2}$>a>0.则$\frac{a^2+b^2}{a-b}$=$\frac{{b}^{4}+4}{2b-{b}^{3}}$=f(b),利用导数研究其单调性极值与最值即可得出.
解答 解:∵b>a>0,ab=2,
∴b>$\sqrt{2}$>a>0.
则$\frac{a^2+b^2}{a-b}$=$\frac{{b}^{4}+4}{2b-{b}^{3}}$=f(b),
f′(b)=$\frac{-{b}^{6}+6{b}^{4}+12{b}^{2}-8}{(2b-{b}^{3})^{2}}$=$\frac{-({b}^{2}+2)[{b}^{2}-(4+2\sqrt{3})][{b}^{2}-(4-2\sqrt{3})]}{(2b-{b}^{3})^{2}}$,
可得:b∈$(\sqrt{2},\sqrt{3}+1)$时,函数f(b)单调递增;b∈$(\sqrt{3}+1,+∞)$时,函数f(b)单调递减.
因此f(b)在b=$\sqrt{3}$+1$(a=\sqrt{3}-1)$时取得最大值,
∴f(b)≤$f(\sqrt{3}+1)$=-4.
∴$\frac{a^2+b^2}{a-b}$的取值范围是(-∞,-4].
故选:A.
点评 本题考查了利用导数研究其单调性极值与最值,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在等腰直角三角形ABC中,AB=AC=1,点E为斜边BC的中点,点M在线段AB上运动,则($\overline{AE}$-$\overline{AM}$)•($\overline{AC}$-$\overline{AM}$)的取值范围是( )
| A. | [$\frac{7}{16}$,$\frac{1}{2}$] | B. | [$\frac{7}{16}$,1] | C. | [$\frac{1}{2}$,1] | D. | [0,1] |
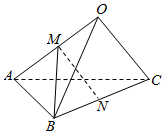 已知三棱锥O-ABC,OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M,N分别是棱OA,BC的中点.求:直线MN与AC所成的角余弦值.
已知三棱锥O-ABC,OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M,N分别是棱OA,BC的中点.求:直线MN与AC所成的角余弦值.