题目内容
18. 如图,三个半径均为r的小球放在一个半球形的碗中,若三个小球的最高点恰好与碗的上沿处于同一水平面.已知这个碗的半径R=3+$\sqrt{21}$,则r=3.
如图,三个半径均为r的小球放在一个半球形的碗中,若三个小球的最高点恰好与碗的上沿处于同一水平面.已知这个碗的半径R=3+$\sqrt{21}$,则r=3.
分析 根据三个小球和碗的相切关系,作出对应的正视图和俯视图,建立球心和半径之间的关系即可得到碗的半径.
解答 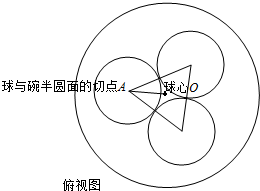 解:分别作出空间几何体的正视图和俯视图如则俯视图中,球心O(也是圆心O)是三个小球与半圆面的三个切点的中心,
解:分别作出空间几何体的正视图和俯视图如则俯视图中,球心O(也是圆心O)是三个小球与半圆面的三个切点的中心,
∵小球的半径为r,
∴三个球心之间的长度为2r,
即OA=$\frac{2\sqrt{3}}{3}$r.
在正视图中,球心B,球心O(同时也是圆心O),
和切点A构成直角三角形,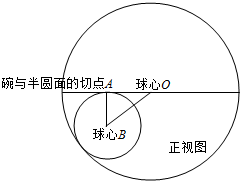
则OA2+AB2=OB2,其中OB=3+$\sqrt{21}$-r,AB=r,
∴($\frac{2\sqrt{3}}{3}$r)2+r2=(3+$\sqrt{21}$-r)2,
∴r=3
故答案为:3.
点评 本题主要考查了球的相切问题 的计算,根据条件作出正视图和俯视图,确定球半径之间的关系是解决本题的关键,综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.长方体ABCD-A1B1C1D1中,有三个面的面积分别为12,20,15,则其外接球球面上的点到平面ABCD的最大距离为( )
| A. | $\frac{9}{2}$ | B. | $\frac{2\sqrt{5}+5}{2}$ | C. | $\frac{2\sqrt{3}+3}{2}$ | D. | $\frac{5\sqrt{2}+5}{2}$ |