题目内容
13．已知函数f（x）为定义在[0，3]上的减函数，则满足f（2x-1）＜f（1）的实数x的取值范围是（ ）| A． | [0，1] | B． | （1，2] | C． | [$\frac{1}{2}$，2] | D． | （1，3] |
分析 根据f（x）为定义在[0，3]上的减函数便可得到$\left\{\begin{array}{l}{0≤2x-1≤3}\\{2x-1＞1}\end{array}\right.$，这样解该不等式组便可得出实数x的取值范围．
解答 解：f（x）为定义在[0，3]上的减函数；
∴由f（2x-1）＜f（1）得：$\left\{\begin{array}{l}{0≤2x-1≤3}\\{2x-1＞1}\end{array}\right.$；
解得1＜x≤2；
∴实数x的取值范围为（1，2]．
故选：B．
点评 考查减函数的定义，函数定义域的概念，不要漏了限制2x-1在定义域内．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
3．已知α=-$\frac{55π}{6}$，则α所在的象限的是（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
4．在等腰直角三角形ABC中，AB=AC=1，点E为斜边BC的中点，点M在线段AB上运动，则（$\overline{AE}$-$\overline{AM}$）•（$\overline{AC}$-$\overline{AM}$）的取值范围是（ ）
| A． | [$\frac{7}{16}$，$\frac{1}{2}$] | B． | [$\frac{7}{16}$，1] | C． | [$\frac{1}{2}$，1] | D． | [0，1] |
18．已知指数函数y=（2a-1）x在（1，+∞）上是减函数，则实数a的取值范围是（ ）
| A． | （$\frac{1}{2}$，1） | B． | （1，+∞） | C． | （-∞，1） | D． | [1，+∞） |
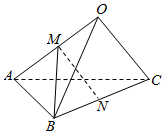已知三棱锥O-ABC，OA=4，OB=5，OC=3，∠AOB=∠BOC=60°，∠COA=90°，M，N分别是棱OA，BC的中点．求：直线MN与AC所成的角余弦值．