题目内容
11．若函数f（x）=$\frac{{x}^{2}+3}{x+1}$，则函数的极值点为1，-3．分析 先求出函数的导数，解关于导函数的方程求出函数的极值点即可．
解答 解：∵函数f（x）=$\frac{{x}^{2}+3}{x+1}$，
∴f′（x）=$\frac{2x（x+1）-{（x}^{2}+3）}{{（x+1）}^{2}}$=$\frac{（x+3）（x-1）}{{（x+1）}^{2}}$，
令f′（x）=0，解得：x=1或-3，
则函数的极值点为1，-3，
故答案为：1，-3．
点评 本题考查了求函数的单调性、极值问题，考查导数的应用，是一道基础题．
练习册系列答案
相关题目
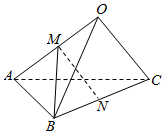已知三棱锥O-ABC，OA=4，OB=5，OC=3，∠AOB=∠BOC=60°，∠COA=90°，M，N分别是棱OA，BC的中点．求：直线MN与AC所成的角余弦值．
20．若将时钟拨快35分钟，那么时针转动的角为（ ）
| A． | 15° | B． | -15° | C． | 18° | D． | -17.5° |
