题目内容
12．如a$\sqrt{a}$+b$\sqrt{b}$＞a$\sqrt{b}$+b$\sqrt{a}$，则a，b必须满足的条件是（ ）| A． | a＞b＞0 | B． | a＜b＜0 | C． | a＞b | D． | a≥0，b≥0，且a≠b |
分析 通过作差、利用根式的意义即可得出．
解答 解：a$\sqrt{a}$+b$\sqrt{b}$-（a$\sqrt{b}$+b$\sqrt{a}$）=（a-b）$（\sqrt{a}-\sqrt{b}）$=$（\sqrt{a}+\sqrt{b}）$$（\sqrt{a}-\sqrt{b}）^{2}$，
又a$\sqrt{a}$+b$\sqrt{b}$＞a$\sqrt{b}$+b$\sqrt{a}$，
则a，b必须满足的条件是a，b≥0，a≠b．
故选：D．
点评 本题考查了作差法、根式的意义，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
3．原点与极点重合，x轴正半轴与极轴重合，则点（2，-2$\sqrt{3}$）的极坐标是（ ）
| A． | （4，$\frac{π}{3}$） | B． | （4，$\frac{4π}{3}$） | C． | （-4，-$\frac{2π}{3}$） | D． | （4，-$\frac{2π}{3}$） |
4．
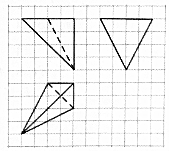如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（ ）
如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（ ）| A． | $\frac{8}{3}$ | B． | $\frac{16}{3}$ | C． | $\frac{32}{3}$ | D． | 16 |
1．如果x2+（y-k+1）2=2表示圆心在y轴负半轴上的圆，那么实数k的一个可能值是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
2．设集合A={x|x2-1＜0}，B={y|y=2x，x∈A}，则A∩B=（ ）
| A． | （0，1） | B． | （$\frac{1}{2}$，1） | C． | （-1，2） | D． | （-1，+∞） |