题目内容
17.将6位学生志愿者分成4组,其中两组各2人,另两组各1人,去四个不同的田径场地服务,不同的服务方案有1080种(用数字作答).分析 根据题意,分2步进行分析:①、先将6人按2-2-1-1分成4组,②、将分好的四组对应分配到四个不同田径场地,由排列、组合数公式计算每一步的情况数目,进而由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①、先将6人按2-2-1-1分成4组,有$\frac{{C}_{6}^{2}{C}_{4}^{2}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}{A}_{2}^{2}}$=45种分组方法,
②、将分好的四组对应分配到四个不同田径场地,有A44=24种方法,
则共有45×24=1080种方法;
故答案为:1080.
点评 本题考查排列、组合的综合应用,注意本题的分组涉及了平均分组与不平均分组两类问题,要用正确使用公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )
如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )
 如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )
如图,网格纸上小正方形的边长是1,在其上用粗线画出了某空间几何体的三视图,则这个空间几何体的体积为( )| A. | π | B. | 2π | C. | 3π | D. | 4π |
12.如a$\sqrt{a}$+b$\sqrt{b}$>a$\sqrt{b}$+b$\sqrt{a}$,则a,b必须满足的条件是( )
| A. | a>b>0 | B. | a<b<0 | C. | a>b | D. | a≥0,b≥0,且a≠b |
9.已知随机变量ξ的分布列为:
若$P({ξ^2}<x)=\frac{11}{12}$,则实数x的取值范围是( )
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{12}$ | $\frac{4}{12}$ | $\frac{1}{12}$ | $\frac{2}{12}$ | $\frac{1}{12}$ |
| A. | 4<x≤9 | B. | 4≤x<9 | C. | x<4或x≥9 | D. | x≤4或x>9 |
6.已知f(x+y)=f(x)+f(y)且f(1)=2,则f(1)+f(2)+…+f(n)不能等于( )
| A. | f(1)+2f(1)+…+nf(1) | B. | f($\frac{n(n+1)}{2}$) | C. | n(n+1) | D. | n(n+1)f(1) |
7.若a=30.3,b=logπ3,c=log0.3e,则( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
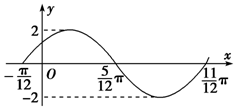 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的一段图象如图所示.
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)的一段图象如图所示.