题目内容
4．
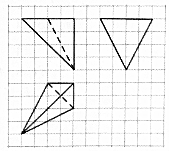如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（ ）| A． | $\frac{8}{3}$ | B． | $\frac{16}{3}$ | C． | $\frac{32}{3}$ | D． | 16 |
分析 根据三视图可知三棱锥倒立放置，从而得出棱锥的高，根据俯视图找出三棱锥的底面，得出底面积，从而可求出棱锥的体积．
解答 解：由主视图和侧视图可知三棱锥倒立放置，棱锥的底面水平放置，故三棱锥的高为h=4，
∵主视图为直角三角形，∴棱锥的一个侧面与底面垂直，
结合俯视图可知三棱锥的底面为俯视图中的左上三角形，∴S底=$\frac{1}{2}×2×4$=4，
∴V=$\frac{1}{3}×4×4$=$\frac{16}{3}$．
故选：B．
点评 本题考查了棱锥的三视图和体积计算，根据三视图的特征找出棱锥的底面是关键，属于中档题．
练习册系列答案
53天天练系列答案
相关题目
14．函数$f（x）=\frac{ax}{{{x^2}+1}}（a＞0）$的单调递增区间是（ ）
| A． | （-∞，-1） | B． | （-1，1） | C． | （1，+∞） | D． | （-∞，-1）∪（1，+∞） |
15．设α=300°，则与α终边相同的角的集合为（ ）
| A． | {α|α=k•360°-30°，k∈Z} | B． | {α|α=k•360°-60°，k∈Z} | ||
| C． | {α|α=k•360°+30°，k∈Z} | D． | {α|α=k•360°+60°，k∈Z} |
12．如a$\sqrt{a}$+b$\sqrt{b}$＞a$\sqrt{b}$+b$\sqrt{a}$，则a，b必须满足的条件是（ ）
| A． | a＞b＞0 | B． | a＜b＜0 | C． | a＞b | D． | a≥0，b≥0，且a≠b |
9．已知随机变量ξ的分布列为：
若$P（{ξ^2}＜x）=\frac{11}{12}$，则实数x的取值范围是（ ）
| ξ | -2 | -1 | 0 | 1 | 2 | 3 |
| P | $\frac{1}{12}$ | $\frac{3}{12}$ | $\frac{4}{12}$ | $\frac{1}{12}$ | $\frac{2}{12}$ | $\frac{1}{12}$ |
| A． | 4＜x≤9 | B． | 4≤x＜9 | C． | x＜4或x≥9 | D． | x≤4或x＞9 |
14．阅读程序框图，运行相应的程序，则输出s的值为（ ）
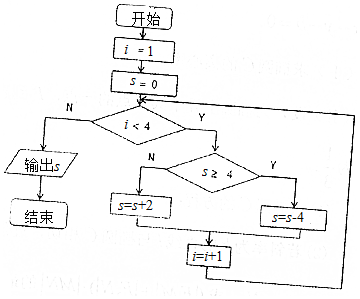
| A． | 0 | B． | 2 | C． | 4 | D． | 6 |