题目内容
设抛物线y2=2px的焦点为F，准线为l点p是抛物线上第一象限内的一点，PA⊥l，垂足为A，若|PF|=2p，则直线PF的斜率是 ．
考点：抛物线的简单性质
专题：直线与圆,圆锥曲线的定义、性质与方程
分析：由已知求出P点坐标，代入斜率公式，可得答案．
解答：
解：∵抛物线y2=2px上的点P是抛物线上第一象限内的一点，
∴p＞0，
又∵|PF|=2p，
∴|PA|=2p，
∴P点的横坐标为
p，代入可得P点的纵坐标为
p，
故kPF=
=
，
故答案为：
∴p＞0，
又∵|PF|=2p，
∴|PA|=2p，
∴P点的横坐标为
| 3 |
| 2 |
| 3 |
故kPF=
| ||||
|
| 3 |
故答案为：
| 3 |
点评：本题考查的知识点是斜率公式，抛物线的性质，难度不大，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
设a＞0，b＞1，若a+b=2，则
+
的最小值为（ ）
| 3 |
| a |
| 1 |
| b-1 |
A、2
| ||
| B、8 | ||
C、4
| ||
D、4+2
|
若复数（a-i）（1+i）是纯虚数（i是虚数单位，a是实数），则a=（ ）
| A、-1 | B、1 | C、±1 | D、0 |
在等差数列{an}中，有a4+a8=a5+a7，类比上述性质，在等比数列{bn}中，有（ ）
| A、b4+b8=b5+b7 |
| B、b4b8=b5b7 |
| C、b4b5=b7b8 |
| D、b4b7=b5b8 |
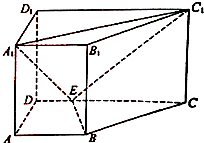如图，直四棱柱中ABCD-A1B1C1D1中，AB∥CD，AD⊥AB，AB=3，AD=1，AA1=2，CD=4，E是CD中点．