题目内容
12.若sinx+siny=1(1)求cos(x-y)的取值范围;
(2)求cosx+cosy取值范围.
分析 (1)由已知可得:0≤sinx≤1、0≤siny≤1,可得:2kπ≤x≤2(k+1)π,2kπ≤y≤2(k+1)π,可求(2k-1)π≤x-y≤2(k+1)π,利用余弦函数的性质即可得解.
(2)由同角三角函数的关系式可得(cosx+cosy)2=1+2cos(x-y)≤1+2*1=3,由-1≤cos(x-y)≤1,即可求得cosx+cosy的取值范围.
解答 解:(1)因为:sinx+siny=1,
所以:0≤sinx≤1、0≤siny≤1,
所以:2kπ≤x≤2(k+1)π,2kπ≤y≤2(k+1)π,
所以:(2k-1)π≤x-y≤2(k+1)π,
所以:-1≤cos(x-y)≤1.
(2)因为,(sinx+siny)2+(cosx+cosy)2=(sin2x+cos2x)+(sin2y+cos2y)+2(cosxcosy+sinxsiny)=2+2cos(x-y),
已知,sinx+siny=1,
可得:(cosx+cosy)2=2+2cos(x-y)-(sinx+siny)2=1+2cos(x-y)≤1+2×1=3,
因为,-1≤cos(x-y)≤1,
所以,-1≤1+2cos(x-y)≤3,
则有:0≤(cosx+cosy)2≤3,
可得:-$\sqrt{3}$≤cosx+cosy≤$\sqrt{3}$,
即有:cosx+cosy的取值范围是[-$\sqrt{3}$,$\sqrt{3}$].
点评 本题主要考察了同角三角函数的关系式的应用,三角函数值域的求法,考查了余弦函数的图象和性质,属于基本知识的考查.

练习册系列答案
相关题目
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$+$\overrightarrow{b}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{5}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
7.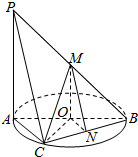 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
①OC∩平面PAC;②MO∥平面PAC;③平面PAC∥平面MON,
其中正确的命题是( )
 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M,N分别为线段PB,BC的中点,有以下三个命题:①OC∩平面PAC;②MO∥平面PAC;③平面PAC∥平面MON,
其中正确的命题是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
17.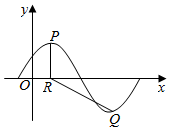 如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )
如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )
 如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )
如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )| A. | $\sqrt{3}$,$\frac{π}{6}$ | B. | $\sqrt{3}$,$\frac{π}{3}$ | C. | 2$\sqrt{3}$,$\frac{π}{6}$ | D. | 2$\sqrt{3}$,$\frac{π}{3}$ |