题目内容
1．已知数列{an}的前四项依次是1，1+2，1+2+22，1+2+22+23，（1）写出该数列的一个通项公式；
（2）该数列从第几项起大于2016？
分析 （1）把数列的前4项写成2的项数次方减1的形式，归纳可得数列的一个通项公式；
（2）由通项大于2016，求得整数n的值得答案．
解答 解：（1）∵1=21-1，1+2=22-1，1+2+22=23-1，1+2+22+23=24-1，
∴数列{an}的一个递推式为${a}_{n}={2}^{n}-1$；
（2）由2n-1＞2016，得2n＞2017，
∵210=1024，211=2048，
∴数列{an}从第11项起大于2016．
点评 本题考查数列递推式，考查了等比数列的前n项和，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．已知集合A={1，2}，B={2，3，4}，那么集合A∩B等于（ ）
| A． | {2} | B． | {2，3} | C． | {1，2，3} | D． | {1，2，3，4} |
9．已知函数f（x）=x-alnx在区间（0，2]上单调递减，则实数a的取值范围是（ ）
| A． | （0，$\frac{1}{2}$） | B． | （0，2） | C． | （$\frac{1}{2}$，+∞） | D． | [2，+∞） |
10．某几何体的三视图如图，则该几何体的体积为（ ）
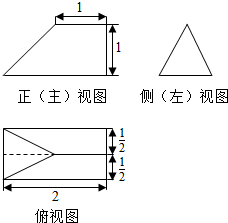
| A． | $\frac{5}{6}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |