题目内容
17.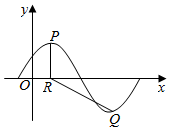 如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )
如图所示为f(x)=Asin($\frac{π}{6}$x+φ)(A>0,0<φ<$\frac{π}{2}$)的部分图象,P,Q分别为f(x)图象的最高点和最低点,点P坐标为(2,A),PR⊥x轴于R,若∠PRQ=$\frac{2π}{3}$.则A及φ的值分别是( )| A. | $\sqrt{3}$,$\frac{π}{6}$ | B. | $\sqrt{3}$,$\frac{π}{3}$ | C. | 2$\sqrt{3}$,$\frac{π}{6}$ | D. | 2$\sqrt{3}$,$\frac{π}{3}$ |
分析 由题意直接求出函数的最大值A,通过点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=$\frac{2π}{3}$,画出图象,求出函数的周期,然后求出最大值,利用函数的图象经过P,求出φ的值.
解答 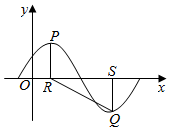 解:如图,∵点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=$\frac{2π}{3}$,
解:如图,∵点P的坐标为(2,A),点R的坐标为(2,0).若∠PRQ=$\frac{2π}{3}$,
∴∠SRQ=$\frac{2π}{3}-\frac{π}{2}$=$\frac{π}{6}$.
则SQ=A,RS=$\frac{T}{2}$=$\frac{π}{\frac{π}{6}}=6$,
则tan$\frac{π}{6}$=$\frac{SQ}{RS}$=$\frac{A}{6}$=$\frac{\sqrt{3}}{3}$,
得A=$2\sqrt{3}$.即P(2,$2\sqrt{3}$),
∴2$\sqrt{3}$=2$\sqrt{3}$sin($\frac{π}{6}×2+ϕ$),解得φ=2kπ+$\frac{π}{2}$-$\frac{π}{3}$,k∈Z,
∵0<φ<$\frac{π}{2}$,
∴当k=0时,φ=$\frac{π}{6}$.
故选:C.
点评 本题考查三角函数的解析式的求法,考查函数的图象的应用,考查计算能力,根据条件结合图象求出A和φ的值是解决本题的关键.

练习册系列答案
相关题目
8.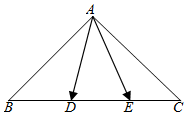 如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )
如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )
 如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )
如图,在等腰直角三角形ABC中,AB=AC=$\sqrt{2}$,D,E是线段BC上的点,且DE=$\frac{1}{3}$BC,则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是( )| A. | $[{\frac{8}{9},\;\frac{4}{3}}]$ | B. | $[{\frac{4}{3},\;\frac{8}{3}}]$ | C. | $[{\frac{8}{9},\;\frac{8}{3}}]$ | D. | $[{\frac{4}{3},\;+∞})$ |
5.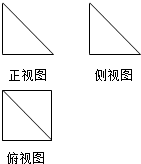 一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
 一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )
一个几何体的三视图如图所示,其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
9.已知函数f(x)=x-alnx在区间(0,2]上单调递减,则实数a的取值范围是( )
| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | ($\frac{1}{2}$,+∞) | D. | [2,+∞) |