题目内容
18．在直角坐标平面内，满足方程$（{y^2}+2|x|）（\frac{x^2}{16}-\frac{y^2}{9}）=0$的点（x，y）所构成的图形为（ ）| A． | 抛物线及原点 | B． | 双曲线及原点 | ||
| C． | 抛物线、双曲线及原点 | D． | 两条相交直线 |
分析 由题意，$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=0，即可得出结论．
解答 解：由题意，$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=0，
∴y=±$\frac{3}{4}$x，
故选：D．
点评 本题考查曲线与方程，考查学生的计算能力，比较基础．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
6．设集合M={x||2x-1|≤3}，N={x∈Z|1＜2x＜8}，则M∩N=（ ）
| A． | （0，2] | B． | （0，2） | C． | {1，2} | D． | {0，1，2} |
如图，OA是南北方向的一条公路，OB是北偏东45°方向的一条公路，某风景区的一段边界为曲线C．为方便游客光，拟过曲线C上的某点分别修建与公路OA，OB垂直的两条道路PM，PN，且PM，PN的造价分别为5万元/百米，40万元/百米，建立如图所示的直角坐标系xoy，则曲线符合函数y=x+$\frac{{4\sqrt{2}}}{x^2}$（1≤x≤9）模型，设PM=x，修建两条道路PM，PN的总造价为f（x）万元，题中所涉及的长度单位均为百米．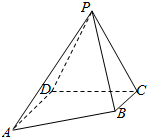
如图，四棱锥P-ABCD中，平面PCD⊥平面ABCD，△PCD是等边三角形，四边形ABCD是梯形，BC∥AD，BC⊥CD，AD=2BC=2$\sqrt{2}$．
7．全称命题：?x∈R，x2≤0的否定是（ ）
| A． | ?x∈R，x2≤0 | B． | ?x0∈R，x${\;}_{0}^{2}$＞0 | C． | ?x0∈R，x${\;}_{0}^{2}$＜0 | D． | ?x0∈R，x${\;}_{0}^{2}$≤0 |