题目内容
8.(1)已知f($\frac{2}{x}$+1)=1gx,求f(x)的解析式;(2)已知f(x)为一次函数,且f[f(x)]=4x+3,求f(x)的解析式.
分析 (1)令$\frac{2}{x}$+1=t则x=$\frac{2}{t-1}$,换元可得;
(2)设一次函数f(x)=ax+b,待定系数可得.
解答 解:(1)令$\frac{2}{x}$+1=t则x=$\frac{2}{t-1}$,
∴f(t)=1g$\frac{2}{t-1}$,
故f(x)的解析式为f(x)=1g$\frac{2}{x-1}$,(x>1);
(2)设一次函数f(x)=ax+b,
由f[f(x)]=4x+3可得a(ax+b)+b=4x+3,
∴a2=4且ab+b=3,解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$或$\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$,
∴f(x)的解析式为f(x)=2x+1或f(x)=-2x-3
点评 本题考查函数解析式求解的换元法和待定系数法,属基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
18.在直角坐标平面内,满足方程$({y^2}+2|x|)(\frac{x^2}{16}-\frac{y^2}{9})=0$的点(x,y)所构成的图形为( )
| A. | 抛物线及原点 | B. | 双曲线及原点 | ||
| C. | 抛物线、双曲线及原点 | D. | 两条相交直线 |
17.设F1、F2分别是双曲线x2-$\frac{{y}^{2}}{9}$=1的左、右焦点,若点P在双曲线上,且向量$\overrightarrow{P{F}_{1}}$与$\overrightarrow{P{F}_{2}}$的夹角为60°,则S${\;}_{△{F}_{1}P{F}_{2}}$=( )
| A. | 9$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 4$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
18.已知a>0,b>0,点(1,2)在直线$\frac{x}{a}$+$\frac{y}{b}$=1上,则a十2b取最小值时,$\frac{b}{a}$=( )
| A. | 2 | B. | 1 | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
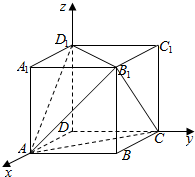 如图,在空间直角坐标系中有单位正方体ABCD-A1B1C1D1.
如图,在空间直角坐标系中有单位正方体ABCD-A1B1C1D1.