题目内容
9.已知等差数列{an}的首项a1=1,公差d≠0且a2,a4,a8成等比数列.数列{bn}的前n项和为Sn且Sn=2bn-2(n∈N*)(1)求数列{an}和{bn}的通项公式;
(2)设数列cn=$\frac{1}{{a}_{n}•{a}_{n+1}}$+log2bn,求数列{cn}的前n项和Tn.
分析 (1)由等差数列通项公式和等比数列性质求出公差,由此能求出数列{an}的通项公式数列,由Sn=2bn-2(n∈N*),得$\frac{{b}_{n}}{{b}_{n-1}}=2(n≥2)$,由此能求出数列{bn}的通项公式.
(2)由cn=$\frac{1}{{a}_{n}•{a}_{n+1}}$+log2bn=$\frac{1}{n(n+1)}+n$=$\frac{1}{n}-\frac{1}{n+1}+n$,利用裂项求和法和分组求和法能求出数列{cn}的前n项和.
解答 解:(1)∵等差数列{an}的首项a1=1,公差d≠0且a2,a4,a8成等比数列,
∴${{a}_{4}}^{2}={a}_{2}{a}_{8}$,即(1+3d)2=(1+d)(1+7d),
解得d=1或d=0(舍),
∴an=1+(n-1)=n.
∵数列{bn}的前n项和为Sn且Sn=2bn-2(n∈N*),
∴当n=1时,S1=b1=2b1-2,解得b1=2,
当n≥2时,bn=Sn-Sn-1=2(bn-bn-1),
整理,得$\frac{{b}_{n}}{{b}_{n-1}}=2(n≥2)$,
∴数列{bn}是以b1=2为首项,2为公比的等比数列,
∴bn=2•2n-1=2n,n∈N*.
(2)由(1)得cn=$\frac{1}{{a}_{n}•{a}_{n+1}}$+log2bn=$\frac{1}{n(n+1)}+n$=$\frac{1}{n}-\frac{1}{n+1}+n$,
∴数列{cn}的前n项和:
Tn=(1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}$)+(1+2+3+…+n)
=1-$\frac{1}{n+1}$+$\frac{n(n+1)}{2}$
=$\frac{n}{n+1}+\frac{n(n+1)}{2}$.
点评 本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.


| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
| 答对题目数 | 小于8 | 8 | 9 | 10 |
| 女 | 2 | 13 | 12 | 8 |
| 男 | 3 | 37 | 16 | 9 |
(Ⅱ)从答对题目数不少于8道的实习期司机中任意选出两人做进一步的调查,求选出的两人中至少有一名女实习期司机的概率.
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 抛物线及原点 | B. | 双曲线及原点 | ||
| C. | 抛物线、双曲线及原点 | D. | 两条相交直线 |
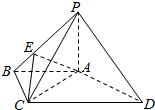 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=90°,且CD=2AB,点E在棱PB上,且PE=2EB,PA=AB=BC. 如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1,AB⊥AC,D为BC中点.AB1与A1B交于点O.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1,AB⊥AC,D为BC中点.AB1与A1B交于点O.