题目内容
计算:
(1)(2
)
-(-9.6)0-(3
)-
+(1.5)-2+(
×
)4;
(2)lg25+lg2×lg500-
lg
-log29×log32.
(1)(2
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
| 2 |
| 3 |
| 2 |
| 4 | 3 |
(2)lg25+lg2×lg500-
| 1 |
| 2 |
| 1 |
| 25 |
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)利用指数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
解答:
解:(1)(2
)
-(-9.6)0-(3
)-
+(1.5)-2+(
×
)4
=
-1-
+
+4×3
=
.
(2)lg25+lg2×lg500-
lg
-log29×log32
=lg25+3+lg5-
×
=lg25+lg5+1.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 8 |
| 2 |
| 3 |
| 2 |
| 4 | 3 |
=
| 3 |
| 2 |
| 4 |
| 9 |
| 4 |
| 9 |
=
| 25 |
| 2 |
(2)lg25+lg2×lg500-
| 1 |
| 2 |
| 1 |
| 25 |
=lg25+3+lg5-
| lg9 |
| lg2 |
| lg2 |
| lg3 |
=lg25+lg5+1.
点评:本题考查指数和对数的化简求值,是基础题,解题时要认真审题,注意运算法则的合理运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
等比数列{an}中,a2=3,a5=
,则公比q=( )
| 1 |
| 9 |
| A、3 | ||
B、
| ||
| C、±3 | ||
D、±
|
下列函数中最小正周期为2π的函数是( )
A、y=sin(x-
| ||
B、y=cos(2x+
| ||
C、y=cos(3x-
| ||
D、y=tan(x-
|
已知
是非零向量,
≠
,则“
•
=
•
”是“
⊥(
-
)”成立的( )
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
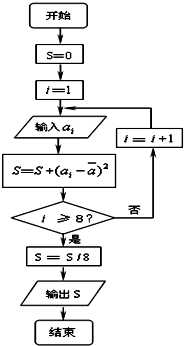 对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为
对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如表所示:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
. |
| a |
| A、5 | B、7 | C、40 | D、56 |
已知x、y均为正数,
+
=1,则xy有( )
| 2 |
| x |
| 8 |
| y |
| A、最大值64 | ||
B、最大值
| ||
| C、最小值64 | ||
D、最小值
|