题目内容

已知
a
是非零向量，
b
≠
c
，则“
a
•
b
=
a
•
c
”是“
a
⊥(
b
-
c
)”成立的（　　）
A、充分非必要条件
B、必要非充分条件
C、非充分非必要条件
D、充要条件
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据“
a
•
b
=
a
•
c
”成立，得到
a
•（
b
-
c
）=0，结合
a
是非零向量，
b
≠
c
，推出
a
⊥(
b
-
c
)，根据充要条件的判定方法可得结论．
解答： 解：∵
a
•
b
=
a
•
c
，
∴
a
•（
b
-
c
）=0，
∵
a
是非零向量，
b
≠
c
，
∴
a
⊥(
b
-
c
)，
故选：D．
点评：题主要考查了数量积判断两个平面向量的垂直关系，以及必要条件、充分条件与充要条件的判断，属于基础题．
练习册系列答案
相关题目
函数y=a1-x（a＞0，a≠1）的图象恒过定点A，若点A在直线mx+2ny-1=0（mn＞0）上，则
1
m
+
1
n
的最小值是
 
．
设正数a，b，c满足
9
a
+
4
b
+
1
c
≤
36
a+b+c
，则
b
a+b+c
=
 
．
在平面直角坐标系中，定义d（A，B）=|x1-x2|+|y1-y2|为两点A（x1，x2），B（y1，y2）的“直角距离”，已知直线l经过点P（
5
，0），倾斜角为α，且cosα=-
5
5
，在直线l上截取线段EF（-
5
≤x≤2
5
），则原点O与线段EF上一点的“直角距离”的最小值与最大值之和是
 
．
计算：
（1）(2
1
4
)
1
2
-(-9.6)0-(3
3
8
)-
2
3
+(1.5)-2+(
2
×
43
)4；
（2）lg25+lg2×lg500-
1
2
lg
1
25
-log29×log32．
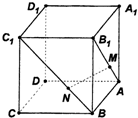如图所示，在正方体ABCD-A1B1C1D1中，点M、N分别在线段AB1、BC1上，且AM=BN．给出下列结论：
①MN与A1C1相交；
②MN∥A1C1；
③MN与A1C1异面，
其中有可能成立的结论的个数为（　　）
A、3B、2C、1D、0
若α是第二象限的角，则角
α
2
所在的象限是（　　）
A、第一象限
B、第二象限
C、第一象限或第二象限
D、第一象限或第三象限
若集合M={x|y=
x
}，且M∪N=M，则集合N可能是（　　）
A、{-1，0，1}
B、{1，2}
C、{x|x≤1}
D、R
已知定圆A：（x+
3
）2+y2=16的圆心A，动圆M过点B（
3
，0），且与圆A相切，动圆的圆心M的轨迹记为C．
（1）求曲线C的方程；
（2）设不垂直于x轴的直线l与上述曲线C交于不同的两点P，Q，点D（-3，0），若x轴是∠PDQ的角平分线，证明直线l过定点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网