题目内容

在棱长为1的正方体ABCD-A1B1C1D1中，动点P在面对角线BC1上，则A1P+PA的最小值为（　　）
A、
6
B、
3+
6
C、1+
2
D、
2
+
3
考点：棱柱的结构特征
专题：函数的性质及应用
分析：将对角面ABC1D1与平面A1BC1放到同一平面，利用平面内两点之间线段最短可求A1P+PA的最小值．
解答： 解：棱长为1的正方体ABCD-A1B1C1D1中，动点P在面对角线BC1上，

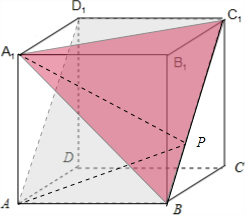
将对角面ABC1D1与平面A1BC1放到同一平面，如下图所示：

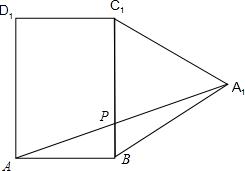
在△ABA1中，BA1=
2
，AB=1，∠ABA1=150°
∴AA1=
AB2+
BA
2
1
-2AB•BA1•cos∠ABA1
=
1+2-2×1×
2
×(-
3
2
)
=
3+
6
，
即A1P+PA的最小值为
3+
6

故选：B
点评：本题的考点是点、线、面间的距离计算，主要考查棱柱的结构特征，考查计算能力，空间想象能力，是基础题．
练习册系列答案
相关题目
已知{an}是等差数列，d为其公差，Sn是其前n项和，若只有S4是{Sn}中的最小项，则可得出的结论中正确的是
 
．
①d＞0    ②a4＜0   ③a5＞0   ④S7＜0    ⑤S8＞0．
已知△ABC的三条边的边长分别为4米、5米、6米，将三边都截掉x米后，剩余的部分组成一个钝角三角形，则x的取值范围是（　　）
A、0＜x＜5
B、1＜x＜5
C、1＜x＜3
D、1＜x＜4
f（x）=2sinπx-x+1的零点个数为（　　）
A、4B、5C、6D、7
数列{an}满足：a1=
1
3
，且对于任意的正整数m，n都有am+n=am•an，则an=（　　）
A、(
1
3
)n-1
B、
2
3
(
1
3
)n-1
C、(
1
3
)n
D、
1
2
[1-(
1
3
)n]
λ，μ∈R，下面式子正确的是（　　）
A、λ
a
与
a
的方向相同
B、（λ+μ）
a
=λ
a
+μ
a
C、0•
a
=0
D、若
b
=λ
a
，则|
b
|=λ
a
若f（x）在[a，b]上连续，在（a，b）内可导，且x∈（a，b）时，f′（x）＞0，又f（a）＜0，则（　　）
A、f（x）在[a，b]上单调递增，且f（b）＞0
B、f（x）在[a，b]上单调递增，且f（b）＜0
C、f（x）在[a，b]上单调递减，且f（b）＜0
D、f（x）在[a，b]上单调递增，但f（b）的符号无法判断
在正项等比数列{an}中，已知a3•a5=12，则a1+a7的最小值为（　　）
A、4
2
B、2
3
C、2
2
D、4
3
若函数f（x）=x2+ax是偶函数，则实数a=（　　）
A、-2B、-1C、0D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网