题目内容
已知△ABC的三条边的边长分别为4米、5米、6米,将三边都截掉x米后,剩余的部分组成一个钝角三角形,则x的取值范围是( )
| A、0<x<5 |
| B、1<x<5 |
| C、1<x<3 |
| D、1<x<4 |
考点:余弦定理
专题:三角函数的求值
分析:根据题意表示出截取后三角形的三边长,设最大角为α,利用余弦定理表示出cosα,利用余弦定理表示出cosα,根据α为钝角,得到cosα小于0,即可确定出x的范围.
解答:
解:根据题意得:截取后三角形的三边长为(4-x)米,(5-x)米,(6-x)米,且长为(6-x)米所对的角为α,α为钝角,
∴cosα=
<0,
整理得:(x-1)(x-4)<0,
解得:1<x<4,
∵4-x>0,5-x>0,6-x>0,且4-x+5-x>6-x,
∴0<x<3,
则x的范围为1<x<3.
故选:C.
∴cosα=
| (4-x)2+(5-x)2-(6-x)2 |
| 2(4-x)(5-x) |
整理得:(x-1)(x-4)<0,
解得:1<x<4,
∵4-x>0,5-x>0,6-x>0,且4-x+5-x>6-x,
∴0<x<3,
则x的范围为1<x<3.
故选:C.
点评:此题考查了余弦定理,以及三角形边角关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点,且面积最小的圆方程为( )
A、(x+
| ||||||
B、(x-
| ||||||
C、(x-
| ||||||
D、(x+
|
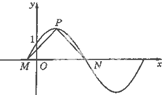 如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤
如图,函数y=2sin(πx+φ),x∈R(其中0≤φ≤| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
在棱长为1的正方体ABCD-A1B1C1D1中,动点P在面对角线BC1上,则A1P+PA的最小值为( )
A、
| ||||
B、
| ||||
C、1+
| ||||
D、
|
抛物线y2=8x与双曲线
-
=1的一个焦点重合,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
| D、4 |
